Home [수치해석] 뉴턴 다항식 보간법
Post
Cancel

[수치해석] 뉴턴 다항식 보간법

Posted Dec 11, 2021 Updated Jun 25, 2022
By DevSlem
35 min read

Introduction

당연하지만 프로그래밍에서 보간법(Interpolation)은 굉장히 중요한 영역이다. 주어진 데이터는 한정적이지만 우리가 예측해야하는 범위는 너무 넓다. 그래서 필요한 것이 보간법 (Interpolation)이다. 예를 들면 다음과 같은 점의 위치를 우리가 이미 알고 있거나 주어졌다고 하자.

\[(-1, 0), (0, 0), (1, 0), (2, 6)\]

위 점을 지나는 함수는 아래와 같다.

\[y = x(x - 1)(x + 1)\]

위 함수의 그래프:

3차함수

위 그림에서 빨간색 점이 우리가 이미 알고 있는 점이고, 위 점을 지나는 유일한 다항함수의 모습은 위와 같은 형태이다.

위 그림의 예처럼 어떠한 데이터가 주어져있을 때 이 데이터들로 부드러운 곡선을 그려 데이터들의 사이값을 예측하고 싶다. 즉, 각 점을 지나는 비선형 함수를 구하고 싶다. 어떤 점들을 지나는 함수를 알 수 있다면 다양하게 활용할 수 있다. 데이터들을 비선형 함수로 보간하는 방법은 여러 개가 있겠지만 여기서는 가장 기초적인 다항식 보간에 대해 설명하려고 한다.

다항식 보간에는 여러가지가 있다. 가장 간단한 방법으로는 주어진 데이터를 가지고 $p(x) = a_0 + a_1x + a_2x^2 + \cdots$ 형태의 방정식을 푸는 게 가장 쉬운 방식이라고 할 수 있다. 행렬을 활용하면 프로그래밍으로 쉽게 각 항의 계수를 구할 수 있다. 이 방법을 Monomial basis 다항식 보간법이라고 한다. 하지만 이 방식에는 몇가지 문제점이 존재하기 때문에 (대표적으로 조건 상수 값이 너무 큼) 다른 다항식 보간법인 뉴턴 다항식 보간법(Newton Polynomial Interpolation)을 소개하려고 한다.

Definition

먼저 미리 말하지만 아래 정의만 보면 무슨 소리인지 이해하기 어려울 것이다. 당황해서 뒤로가기 누르지 말고 가볍게 보기를 권장한다. $n + 1$개의 Point에 대한 데이터 집합이 아래와 같이 주어져 있다고 하자.

\[(x_0, y_0), (x_1, y_1), \cdots, (x_n, y_n)\]

위 $n + 1$개의 Point 중 $x$ 좌표가 모두 다르다면 뉴턴 다항식은 다음과 같이 정의될 수 있다.

\[N(x) = \displaystyle\sum_{i = 0}^{n}a_i p_i(x)\]

$p_i(x)$는 Newton basis polynomials (뉴턴 기반 다항식)이며 아래와 같이 정의된다.

\[p_i(x) = \displaystyle\prod_{k = 0}^{i - 1}(x - x_k)\]

다항식의 형식이 변수 $x$에서 위 Point의 $x$좌표를 뺀 항들끼리 곱해지는 형태이다.
이 때 주의깊게 볼 점은 $i$번 째 뉴턴 기반 다항식에 대해서 $i - 1$번째까지의 $x$좌표를 참조한다. 이를 유의해야 한다.

각 항의 계수 $a_i$는 Divided differences(분할 차분)이며 아래와 같이 정의된다.

\[f[x_k] = f(x_k)\] \[f[x_k, x_{k + 1}, \cdots, x_l] = \displaystyle\frac{f[x_{k + 1}, \cdots, x_l] - f[x_k, \cdots, x_{l - 1}]}{x_l - x_k}\] \[f[x_k, \cdots, x_l] = f[x_l, \cdots, x_k]\] \[a_i = f[x_0, x_1, \cdots, x_i]\]

위 정의를 종합하면 뉴턴 다항식을 조금 쉽게 풀어 쓸 수 있다.

\[\begin{aligned} N(x) &= a_0 + a_1(x - x_0) + a_2(x - x_0)(x - x_1) + \cdots + a_n(x - x_0)(x - x_1)\cdots(x - x_{n - 1}) \\ &= f[x_0] + f[x_0, x_1] (x - x_0) + f[x_0, x_1, x_2] (x - x_0)(x - x_1)+ \cdots \\ &+ f[x_0, x_1, \cdots, x_n] (x - x_0)(x - x_1)\cdots(x - x_{n - 1}) \end{aligned}\]

How to calculate Divided Differences

앞의 Definition에서는 $n + 1$개의 Point가 있다고 가정했지만 지금부터는 $n$개의 데이터가 있으며 모든 인덱스는 0부터 시작한다고 가정할 것이다. 이는 코딩의 편의성을 위해서이다. 즉, 주어진 Point는 아래와 같다고 가정한다.

\[(x_0, y_0), (x_1, y_1), \cdots, (x_{n - 1}, y_{n - 1})\]

분할차분 정의 해석

분할차분의 정의 중 아래 식에서 한가지 특징을 알 수 있다.

\[f[x_k, x_{k + 1}, \cdots, x_l] = \displaystyle\frac{f[x_{k + 1}, \cdots, x_l] - f[x_k, \cdots, x_{l - 1}]}{x_l - x_k}\]

$l > k$라고 가정 할 때 좌측 항의 분할차분의 경우 $x_k, \cdots, x_l$까지 총 $l - k + 1$개의 $x$를 참조하지만 (설명의 편의를 위해 참조란 용어를 사용했지만 실제로 각 $x_i$의 값을 직접 참조하는 것은 아니다), 우측 항에서는 각 2개의 분할차분 모두 1개가 줄어든 $l - k$개의 $x$를 참조한다. 즉, 식을 전개할 수록 $x$를 참조하는 일종의 스케일이 줄어드는 재귀적 관계이다. 다만 아직까지 감이 안잡힐 수도 있으니 간단한 예를 들어보겠다.

\[f[x_0, x_1, x_2] = \displaystyle\frac{f[x_1, x_2] - f[x_0, x_1]}{x_2 - x_0}\]

위 식에서 $k = 0, l = 2$이다. 좌측항은 $x_0, x_1, x_2$를 참조하지만 우측항의 분할차분은 각각 $x_0, x_1$와 $x_1, x_2$를 참조한다. 위 식의 우측항에 있는 각각의 분할차분 식을 다시 아래에 전개해보겠다.

\[f[x_1, x_2] = \displaystyle\frac{f[x_2] - f[x_1]}{x_2 - x_1}\] \[f[x_0, x_1] = \displaystyle\frac{f[x_1] - f[x_0]}{x_1 - x_0}\]

위 식에서 또다시 스케일이 줄어들었다. $f[x_k] = f(x_0)$로 분할차분이 최소단위가 됬음을 확인할 수 있다.

분할차분 계산

이제 본격적으로 위 예를 가지고 분할차분 값을 계산해보겠다. 아래 분할차분의 정의를 활용하는 것으로부터 분할차분 계산을 시작할 수 있다.

\[f[x_k] = f(x_k)\]

위 정의를 활용하면 각각의 분할차분을 계산할 수 있다.

\[f[x_1, x_2] = \displaystyle\frac{f[x_2] - f[x_1]}{x_2 - x_1} = \displaystyle\frac{f(x_2) - f(x_1)}{x_2 - x_1}\] \[f[x_0, x_1] = \displaystyle\frac{f[x_1] - f[x_0]}{x_1 - x_0} = \displaystyle\frac{f(x_1) - f(x_0)}{x_1 - x_0}\]

우리는 $x$좌표와 그에 대응하는 함수값 $f(x)$또는 $y$좌표를 이미 알고 있다. 따라서 위 분할차분을 계산할 수 있다. 참고로 위 분할차분의 특징은 함수의 평균변화율 혹은 두 점 사이의 직선의 기울기이다. 필요한 2개의 분할차분 값을 구했으니 이를 활용해 다음 분할차분값을 드디어 구할 수 있다.

\[f[x_0, x_1, x_2] = \displaystyle\frac{f[x_1, x_2] - f[x_0, x_1]}{x_2 - x_0}\]

위 식에서 $f[x_1, x_2]$와 $f[x_0, x_1]$는 이미 구해서 알고 있고 $x$좌표 역시 원래 알고 있던 값이므로 $f[x_0, x_1, x_2]$ 값을 구하는 거는 단순 계산일 뿐이다.

우리는 지금까지 분할차분을 구하는 방법을 알아보았다. 하지만 위 방식만 가지고는 구하기도 다소 어렵고, 코딩에 적용하기도 쉽지 않다. 따라서 우리는 분할차분표라는 개념을 도입해 문제를 쉽게 해결해보려 한다.

Divided Differences Table

Divided Differences Table은 분할차분표로 위에서 소개한 bottom-up 방식의 계산을 table 형태의 자료구조를 통해 쉽게 계산할 수 있도록 해주는 방법이다. 표의 형태는 아래와 같다.

분할차분표:

$x_i$$f[x_i]$$f[x_i, x_{i + 1}]$$f[x_i, x_{i + 1}, x_{i + 2}]$$f[x_i, x_{i + 1}, x_{i + 2}]$$\cdots$$f[x_i, \cdots, x_{i + (n - 1)}]$
$x_0$$f(x_0)$$f[x_0, x_1]$$f[x_0, x_1, x_2]$$f[x_0, x_1, x_2, x_3]$$\cdots$$f[x_0, x_1, \cdots, x_{n - 1}]$
$x_1$$f(x_1)$$f[x_1, x_2]$$f[x_1, x_2, x_3]$$\vdots$  
$x_2$$f(x_2)$$f[x_2, x_3]$$\vdots$   
$x_3$$f(x_3)$$\vdots$    
$\vdots$$\vdots$     
$x_{n - 1}$$f(x_{n - 1})$     

$n$개의 Point(점)가 있고, 분할차분표의 행 인덱스는 $i$, 열 인덱스는 $j$이며 0부터 시작한다. 위 분할차분표의 특징은 아래와 같다.

  • 분할차분 값에 해당되는 부분은 $n \times n$ table로 구성된다.
  • 각 열의 원소 개수는 $n$개에서 $j$개씩 감소한다. 즉, $n - j$개이다.

분할차분표를 이용한 계산

분할차분표를 활용해 분할차분을 쉽게 계산하는 방법을 소개한다. 분할차분 계산에서 들었던 예시를 분할차분표를 이용해 구해보겠다. 또한 이해를 돕기 위해 표에 행과 열에 대한 인덱스를 추가했다.

가장 먼저 우리가 이미 알고 있는 값인 Point의 $x$좌표와 $y$좌표를 표에 넣는다.

 Column012
Row$x_i$$f[x_i]$$f[x_i, x_{i + 1}]$$f[x_i, x_{i + 1}, x_{i + 2}]$
0$x_0$$f(x_0)$  
1$x_1$$f(x_1)$  
2$x_2$$f(x_2)$  

분할차분 계산에서 이미 봤듯이 분할차분 값을 계산하는 핵심은 이전의 분할차분 값을 이용하는 거다. 이 때 현재 열의 분할차분 값을 구하기 위해서는 직전 열의 바로 옆에 있는 값과 그 아래 값을 이용한다. 즉, $i$행 $j$열의 분할차분 값을 구하기 위해서 $i$행 $j - 1$열의 값과 $i + 1$행 $j - 1$열의 분할차분 값을 참조한다. 아래 표를 보면 조금 더 쉽게 이해할 수 있다. 참조해야하는 분할차분 값에 화살표를 그렸다.

 Column012
Row$x_i$$f[x_i]$$f[x_i, x_{i + 1}]$$f[x_i, x_{i + 1}, x_{i + 2}]$
0$x_0$$f(x_0)$ $\rightarrow$$f[x_0, x_1] = \displaystyle\frac{f[x_1] - f[x_0]}{x_1 - x_0}$ 
1$x_1$$f(x_1)$ $\nearrow$  
2$x_2$$f(x_2)$  
 Column012
Row$x_i$$f[x_i]$$f[x_i, x_{i + 1}]$$f[x_i, x_{i + 1}, x_{i + 2}]$
0$x_0$$f(x_0)$$f[x_0, x_1] = \displaystyle\frac{f[x_2] - f[x_0]}{x_1 - x_0}$ 
1$x_1$$f(x_1)$ $\rightarrow$$f[x_1, x_2] = \displaystyle\frac{f[x_2] - f[x_1]}{x_2 - x_1}$ 
2$x_2$$f(x_2)$ $\nearrow$  

이제 위에서 구한 두 분할차분 값 $f[x_0, x_1]$과 $f[x_1, x_2]$를 가지고 $f[x_0, x_1, x_2]$를 구하면 된다. 또한 분모의 경우 $f[x_0, x_1, x_2]$에서 맨 왼쪽의 $x_0$와 맨 오른쪽의 $x_2$의 값의 차인 $x_2 - x_0$로 구할 수 있다. 분모가 왜 이렇게 구해지는지 기억이 나지 않을 경우 분할차분 정의 해석을 보고 오기 바란다.

 Column012
Row$x_i$$f[x_i]$$f[x_i, x_{i + 1}]$$f[x_i, x_{i + 1}, x_{i + 2}]$
0$x_0$$f(x_0)$$f[x_0, x_1]$ $\rightarrow$$f[x_0, x_1, x_2] = \displaystyle\frac{f[x_1, x_2] - f[x_0, x_1]}{x_2 - x_0}$
1$x_1$$f(x_1)$$f[x_1, x_2]$ $\nearrow$ 
2$x_2$$f(x_2)$  

이제 우리는 뉴턴 다항식 보간을 위해 필요한 모든 분할차분 값을 구할 수 있게 되었다.

분할차분표를 활용해 다항식 보간하기

뉴턴 다항식은 앞에서 봤지만 다시 Remind하자. 앞의 정의에서는 $n + 1$개의 Point였지만 지금은 $n$개의 Point이기 때문에 개수에 맞춰서 식을 다시 작성했다.

\[\begin{aligned} N(x) &= f[x_0] + f[x_0, x_1] (x - x_0) + f[x_0, x_1, x_2] (x - x_0)(x - x_1)+ \cdots \\ &+ f[x_0, x_1, \cdots, x_{n - 1}] (x - x_0)(x - x_1)\cdots(x - x_{n - 2}) \end{aligned}\]

뉴턴 다항식에서 $k$가 $0 \leq k \leq n - 1$ 조건을 만족할 때, $k$번째 항의 계수는 $f[x_0, \cdots, x_k]$이며 모든 항의 계수인 분할차분은 $x_0$부터 시작한다. 분할 차분표에서 $i$행 $j$열의 분할차분은 $f[x_i, \cdots, x_{i + j}]$이다. 즉, 뉴턴 다항식의 $k$번째 항의 계수는 0행 $k$열의 분할차분 값이다.

아래는 앞서 구한 분할차분표 예시이다.

 Column012
Row$x_i$$f[x_i]$$f[x_i, x_{i + 1}]$$f[x_i, x_{i + 1}, x_{i + 2}]$
0$x_0$0번째 항의 계수: $f(x_0)$1번째 항의 계수: $f[x_0, x_1]$2번째 항의 계수: $f[x_0, x_1, x_2]$
1$x_1$$f(x_1)$$f[x_1, x_2]$ 
2$x_2$$f(x_2)$  

위 분할차분표를 가지고 뉴턴 다항식을 보간하면 아래와 같다.

\[N(x) = f(x_0) + f[x_0, x_1] (x - x_0) + f[x_0, x_1, x_2] (x - x_0)(x - x_1)\]

임의의 점 3개가 주어졌을 때 분할차분표를 활용하면 위와 같이 2차함수로 보간할 수 있다.

거창하게 뉴턴 다항식, 분할차분과 같은 어려운 개념을 봤지만, 결국 우리가 구한 식을 보면 단순한 다항식이다. 나름 굉장히 복잡한 원리를 통해서 다항식을 도출해지만 사실 다항식을 구하는 방법은 Introduction에서 말했듯이 단순하게 $y = a_0 + a_1x + a_2x^2 + \cdots$ 형태의 방정식에 지나는 점을 대입해 각 항의 계수를 구하는 것이 훨씬 쉽고 간편하다. 하지만 이 방법은 코딩 시 가우스 소거법과 같은 행렬 연산을 통해 방정식을 풀어야 하는데, 데이터의 개수가 많아질 경우 오차에도 취약해지고 속도가 굉장히 느려진다. 따라서 더 나은 대안인 뉴턴 다항식 보간을 활용하는 것이다.

Algorithm

지금까지 분할차분의 개념, 분할차분표를 통한 분할차분의 계산, 뉴턴 다항식 보간 등을 알아보았다. 이제 뉴턴 다항식 보간에 대한 알고리즘을 소개하고 이를 코딩해보려 한다. 알고리즘은 아래와 같다.

$\text{Algorithm: Newton polynomial interpolation}$

\(\begin{align*} & \textstyle \text{Input: a point set } P = (x_0, y_0), \cdots, (x_{n-1}, y_{n-1}) \text{ of } n \text{ points, target } x \\ & \textstyle \text{Initialize a } n \times n \text{ table } T \in \mathbb{R}^{n \times n}, \ T_{i,0} \leftarrow y_i \text{ for all } i \\ \\ & \textstyle \text{for } j = 1 \text{ to } n - 1 \text{ do} \\ & \textstyle \qquad \text{for } i = 0 \text{ to } n - 1 - j \text{ do} \\ & \textstyle \qquad\qquad T_{i,j} \leftarrow (T_{i+1,j-1} - T_{i,j-1}) / (x_{i+j} - x_i) \\ & \textstyle \qquad \text{end} \\ & \textstyle \text{end} \\ \\ & \textstyle N \leftarrow 0 \\ & \textstyle p \leftarrow 1 \\ & \textstyle \text{for } i = 0 \text{ to } n - 1 \text{ do} \\ & \textstyle \qquad N \leftarrow N + T_{0,i} \times p \\ & \textstyle \qquad p \leftarrow p \times (x - x_{i}) \\ & \text{end} \\ \\ & \textstyle \text{return } N \end{align*}\)

위 알고리즘을 활용해 실제 코드로 구현해보자.

Python Code

Algorithm의 내용을 Python 코드로 구현한다. Numpy library를 활용하였다.

1

import numpy as np

분할차분표 Method - Python

point set points을 입력하면 분할차분표를 계산 후 반환한다. Numpy의 장점을 활용하기 위해 Algorithm 파트와 같이 중첩 for문을 사용하지 않고 각 열에 대해 vectorization 기법을 활용하여 계산하였다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def divided_differences_table(points: np.ndarray):
    assert points.ndim == 2 and points.shape[1] == 2
    
    x = points[:, 0]
    y = points[:, 1]
    n = points.shape[0]
    # Initialize divided differences table
    T = np.zeros((n, n))
    T[:, 0] = y
    for j in range(1, n):
        l = n - j # last row of a current colummn
        T[:l, j] = (T[1:l+1, j-1] - T[:l, j-1]) / (x[j:j+l] - x[:l])
        
    return T

위 for문에서 지역변수 l은 현재 분할차분을 계산하려는 열에 대해 마지막 행으로 i로 생각하면 사실상 수식은 동일하다.

뉴턴 다항식 보간 - Python

newton_poly()는 입력된 point set points에 대해 뉴턴 다항식을 반환하는 method이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def newton_poly(points: np.ndarray):
    assert points.ndim == 2 and points.shape[1] == 2
    
    T = divided_differences_table(points)
    coef = T[0, :] # coefficients from the first row of divided differences table
    x_values = points[:, 0]
    
    def interpolate(x):
        try:
            iter(x)
            x = np.array(x)
            N = np.zeros_like(x)
            p = np.ones_like(x)
        except TypeError:
            N = 0
            p = 1

        for i in range(len(coef)):
            N += coef[i] * p
            p *= x - x_values[i]
        
        return N
    
    return interpolate

위에서 정의한 divided_differences_table() method를 통해 분할차분표를 획득한 뒤 뉴턴 다항식 보간에 사용할 계수를 추출한다. local function interpolate()에 coef와 x_values를 capture 시킨 뒤 뉴턴 다항식을 계산 방법을 기술한다. 이 때 interpolate()의 입력 x에도 vectorization을 지원하기 위해 Numpy의 utility function들을 활용하였다. 그 후 interpolate() local function 자체를 반환하면 입력된 point set에 대한 뉴턴 다항식 자체를 획득할 수 있다.

뉴턴 다항식 보간 최종 코드 - Python

위 내용을 정리한 코드이다.

디버깅 - Python

디버깅을 위해 우리가 잘 알고 있는 3차함수인 $y = x(x - 1)(x + 1)$를 지나는 Point들을 Point2 타입의 배열을 만들고 초기화 한다. 점이 4개이기 때문에 3차함수를 보간할 수 있다.

1
2
3
4
5
6
7

p = np.array([[-1, 0],
              [0, 0],
              [1, 0],
              [2, 6]])

func = newton_poly(p)
print(func([-2.0, 3.0]))

출력된 결과는 다음과 같다.

보간하고자 했던 함수에 동일한 $x$값인 -2와 3을 대입해보면 동일한 함숫값을 얻을 수 있다. 즉, 성공적으로 다항식을 보간했다. 이제 어떤 임의의 점이든지 간에 그 점들을 지나는 유일한 다항함수를 결정할 수 있다.

Matplotlib로 뉴턴 다항식 그래프 출력 - Python

위 보간된 뉴턴 다항식을 그래프로도 확인해보자.

1
2
3
4
5
6
7

import matplotlib.pyplot as plt

x = np.linspace(-3.0, 3.0, 100)
y = func(x)
plt.plot(x, y)
plt.scatter(p[:,0], p[:,1], c="r", marker="o")
plt.show()

뉴턴 다항식 그래프:

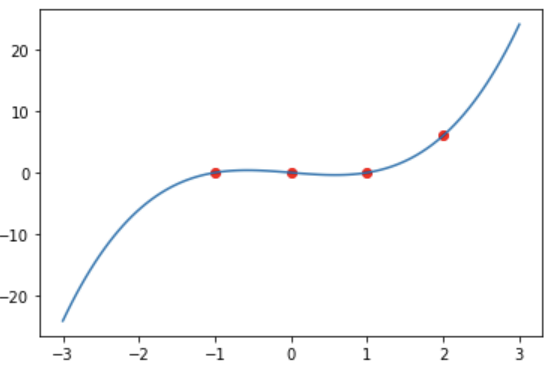
보간된 뉴턴 다항식은 주어진 point set p를 지나감을 확인할 수 있다.

C# Code

Unity에서 사용해 보기 위해 C#으로도 구현해보았다.

사용자 정의 타입 선언 - C#

먼저 2차원 상의 Point의 위치를 표현할 수 있는 Point2 struct를 정의한다.

1
2
3
4
5
6
7
8
9
10
11

struct Vector2
{
    public float x;
    public float y;

    public Vector2(float x, float y)
    {
        this.x = x;
        this.y = y;
    }
}

다음은 입력으로 $x$값을 받고, 출력으로 함숫값을 반환하는 delegate를 선언한다. delegate 타입은 InterpolatedFunction이라고 명칭하겠다. 이는 뉴턴 다항식 보간 시 보간된 다항식을 반환하기 위한 대리자이다.

1
2

// 입력: x, 출력: f(x)
delegate float InterpolatedFunction(float x);

뉴턴 다항식 보간 메소드 선언 - C#

구현하려는 뉴턴 다항식 보간 메소드의 형식은 다음과 같다.

  • Point2 타입의 배열을 points 매개변수에 입력받는다. points 배열은 Point의 집합이다.
  • points 배열의 각 점을 지나는 다항식 험수를 보간 후 보간된 다항식을 반환한다.

위 내용을 수학적으로 정리하면 다음과 같다.

  • 입력: points 배열
    $(x_0, y_0), (x_1, y_1), \cdots$
  • 출력: 보간된 뉴턴 다항식
    $N(x) = f[x_0] + f[x_0, x_1] (x - x_0) + f[x_0, x_1, x_2] (x - x_0)(x - x_1)+ \cdots$

즉, 위 $N(x)$ 함수를 InterpolatedFunction delegate에 할당 후 반환하려는 것이다. 아래는 뉴턴 다항식 보간 메소드이다.

1

static InterpolatedFunction NewtonPolynomial(params Vector2[] points) {  }

이제 위 메소드를 구현할 시간이다.

분할차분표 생성 및 초기화 - C#

먼저 분할차분표를 2차원 배열로 구현한다. $n$개의 Point가 주어졌다면 $n - 1$차 다항식을 보간할 수 있으며 분할차분표의 크기는 $n$행 $n$열이다. 이 때 각 행과 열의 인덱스 범위는 $0 \leq i, j \leq n - 1$이다. 분할차분표에는 $x$좌표는 들어가지 않으며 오직 분할차분 값만 들어간다.

1
2

int n = points.Length; // Point의 개수
float[,] dividedDifferenceTable = new float[n, n]; // n행 n열 크기의 분할차분표

분할차분표의 0번째 열은 $f[x_i] = f(x_i)$이므로 각 Point의 $y$좌표(또는 함수값)을 대입한다.

1
2
3
4
5

// 0번째 열에 y좌표(함수값) 대입
for (int i = 0; i < n; i++)
{
    dividedDifferenceTable[i, 0] = points[i].y;
}

$i$행 $j$열의 분할차분 값은 $i + 1$행 $j - 1$열의 분할차분과 $i$행 $j - 1$열의 분할차분을 통해 구한다. 즉, 분할차분표의 $i$행 $j$열의 값을 $T_{i, j}$라고 할 때 $T_{i, j} = \displaystyle\frac{T_{i + 1, j - 1} - T_{i, j - 1}}{x_{i + j} - x_i}$이다. 또한 $i + 1$행 $j - 1$열의 분할차분 참조로 인해 각 열의 원소 개수는 $n - j$개다. 따라서 각 열에 대해 $i$는 $0$부터 $n - 1 - j$까지 참조한다. 내용이 잘 이해되지 않는다면 분할차분표를 이용한 계산을 다시 보길 권장한다.

1
2
3
4
5
6
7
8
9

// 분할 차분 값들을 이전 분할 차분 값으로부터 순차적으로 구함
// 0번째 열은 이미 구했으므로 j = 1부터 시작
for (int j = 1; j < n; j++)
{
    for (int i = 0; i < n - j; i++)
    {
        dividedDifferenceTable[i, j] = (dividedDifferenceTable[i + 1, j - 1] - dividedDifferenceTable[i, j - 1]) / (points[i + j].x - points[i].x);
    }
}

뉴턴 다항식 보간 - C#

분할차분표를 완성했기 때문에 이제 뉴턴 다항식을 보간할 수 있다. 분할차분표의 0번째 행이 뉴턴 다항식의 각 항의 계수이다. 메모리 효율성을 위해 전처리로 분할차분표의 0번째 행과 Points의 $x$값들을 따로 복사한다. 그 이유는 delegate나 local function 사용 시 변수를 캡쳐할 때 발생하는 몇가지 문제 때문이다. 자세한 내용은 C# 클로저 개념을 참조하면 되며 이 포스트의 주 목적은 아니기 때문에 크게 신경쓰지 않아도 된다.

1
2
3
4
5
6
7
8
9
10
11
12
13

// 보간하려는 다항함수의 계수: 분할차분표의 0번째 행
float[] coef = new float[n];
for (int i = 0; i < n; i++)
{
    coef[i] = dividedDifferenceTable[0, i];
}

// 필요한 데이터의 x값(마지막 x값은 필요 없음)
float[] x_points = new float[n - 1];
for (int i = 0; i < n - 1; i++)
{
    x_points[i] = points[i].x;
}

뉴턴 다항식을 구하는 Interpolate() local function 내부에서 뉴턴 다항식 $N(x) = f[x_0] + f[x_0, x_1] (x - x_0) + f[x_0, x_1, x_2] (x - x_0)(x - x_1) + \cdots$ 와 같이 각 항의 차수가 순차적으로 증가하는 형태로 다항식을 보간한다. 이 때 위에서 복사한 값을 활용해 뉴턴 다항식을 보간할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13

float Interpolate(float x)
{
    float functionValue = 0f; // 반환할 함수값
    float newtonBasisPoly = 1f; // 뉴턴 기반 다항식

    for (int i = 0; i < coef.Length; i++)
    {
        functionValue += coef[i] * newtonBasisPoly;
        newtonBasisPoly *= x - x_points[i]; // 누적곱을 사용함
    }

    return functionValue;
}

local function Interpolate()를 InterpolatedFunction delegate 인스턴스에 할당 후 반환한다. 이렇게 처리하는 목적은 동일한 data set에 대해 중복해서 분할차분표를 구하는 낭비를 피하기 위해서이다.

1

return new InterpolatedFunction(Interpolate);

뉴턴 다항식 보간 최종 코드 - C#

위 내용을 정리한 코드이다.

디버깅 - C#

디버깅을 위해 우리가 잘 알고 있는 3차함수인 $y = x(x - 1)(x + 1)$를 지나는 Point들을 Point2 타입의 배열을 만들고 초기화 한다. 점이 4개이기 때문에 3차함수를 보간할 수 있다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

static void Main(string[] args)
{
    Vector2[] points = new Vector2[4]
    {
        new Vector2(-1, 0),
        new Vector2(0, 0),
        new Vector2(1, 0),
        new Vector2(2, 6)
    };

    var f = NewtonPolynomial(points); // 뉴턴 다항식 보간 메소드 호출

    // 결과: (-2, -6), (3, 24)
    Console.WriteLine($"({-2}, {f(-2)}), ({3}, {f(3)})");
}

출력된 결과는 다음과 같다.

\[(-2, -6), (3, 24)\]

보간하고자 했던 함수에 동일한 $x$값인 -2와 3을 대입해보면 동일한 함숫값을 얻을 수 있다. 즉, 성공적으로 다항식을 보간했다. 이제 어떤 임의의 점이든지 간에 그 점들을 지나는 유일한 다항함수를 결정할 수 있다.

Unity에서 구현한 비선형 오브젝트(함정) - C#

Unity Object를 주어진 데이터에 의해 보간된 비선형 함수의 궤적을 따라 움직이도록 구현하였다.

인스펙터 설정

데이터 입력과 보간, 이동 기능은 아래 Non Linear Movable Object 컴포넌트에서 처리했다.

  • 4개의 점을 입력해 각 점을 지나는 3차함수를 보간한다. 3차함수 인스펙터

  • 5개의 점을 입력해 각 점을 지나는 4차함수를 보간한다. 4차함수 인스펙터

실제 이동 장면

아래는 각각 3차함수와 4차함수의 궤적으로 움직이는 함정을 보여주는 장면이다.

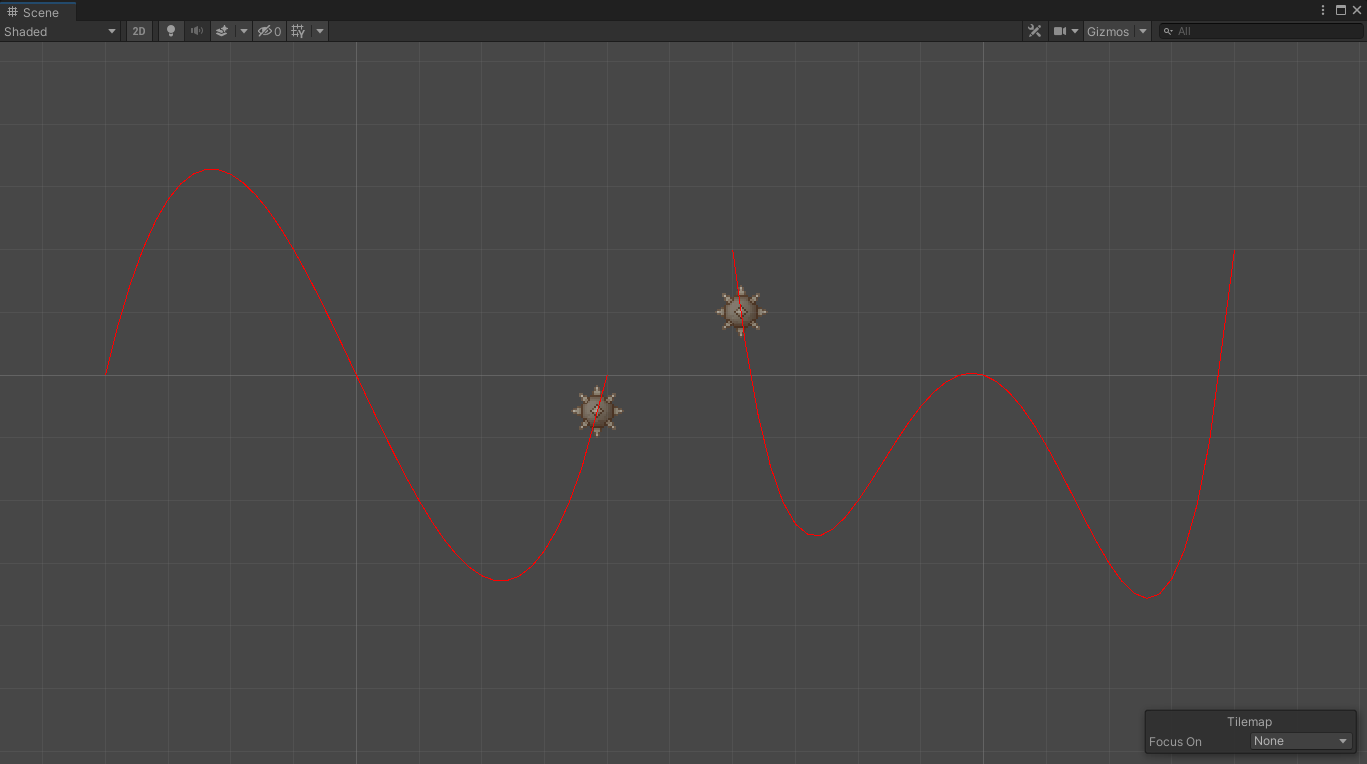
Non Linear Object

직선 방향으로만 움직이는 함정보다 위와 같이 곡선 형태의 움직임을 취하면 좀 더 다양성을 줄 수 있고 게임 난이도도 올릴 수 있다.

References

[1] Wikipedia. Newton polynomial.
[2] INU. Jibum Kim. 수치해석 lecture.

Numerical Analysis
Interpolation Algorithm Unity C# Python
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents