이 포스트에서는 deep RL의 기본이자 시대를 열어준 DQN(Deep Q-Networks)을 도입한 Playing Atari with Deep Reinforcement Learning 논문에 대해 소개한다.
Introduction
DQN 이전에는, 강화학습에서 사용되는 Q-learning과 같은 tabular method는 state와 action space가 작은 경우에만 사용할 수 있었다. 몰론, DQN 이전에도 function approximation method가 있긴 했지만 한계가 뚜렸했다. 특히, 이미지와 같은 high-dimensional 입력으로부터 직접적으로 Q-value를 추정하는 것은 어려운 문제였다. 그러나 딥러닝의 발전으로 인해 high-dimensional raw data로부터 high-level feature를 추출하는 것이 가능해졌다. DQN은 이러한 딥러닝의 강력한 능력을 강화학습에 적용하고자 한 최초의 사례이다. DQN이 기존 tabular Q-learning과의 차이점은 action-value를 추정하기 위해 deep neural network를 사용한다는 것이다:
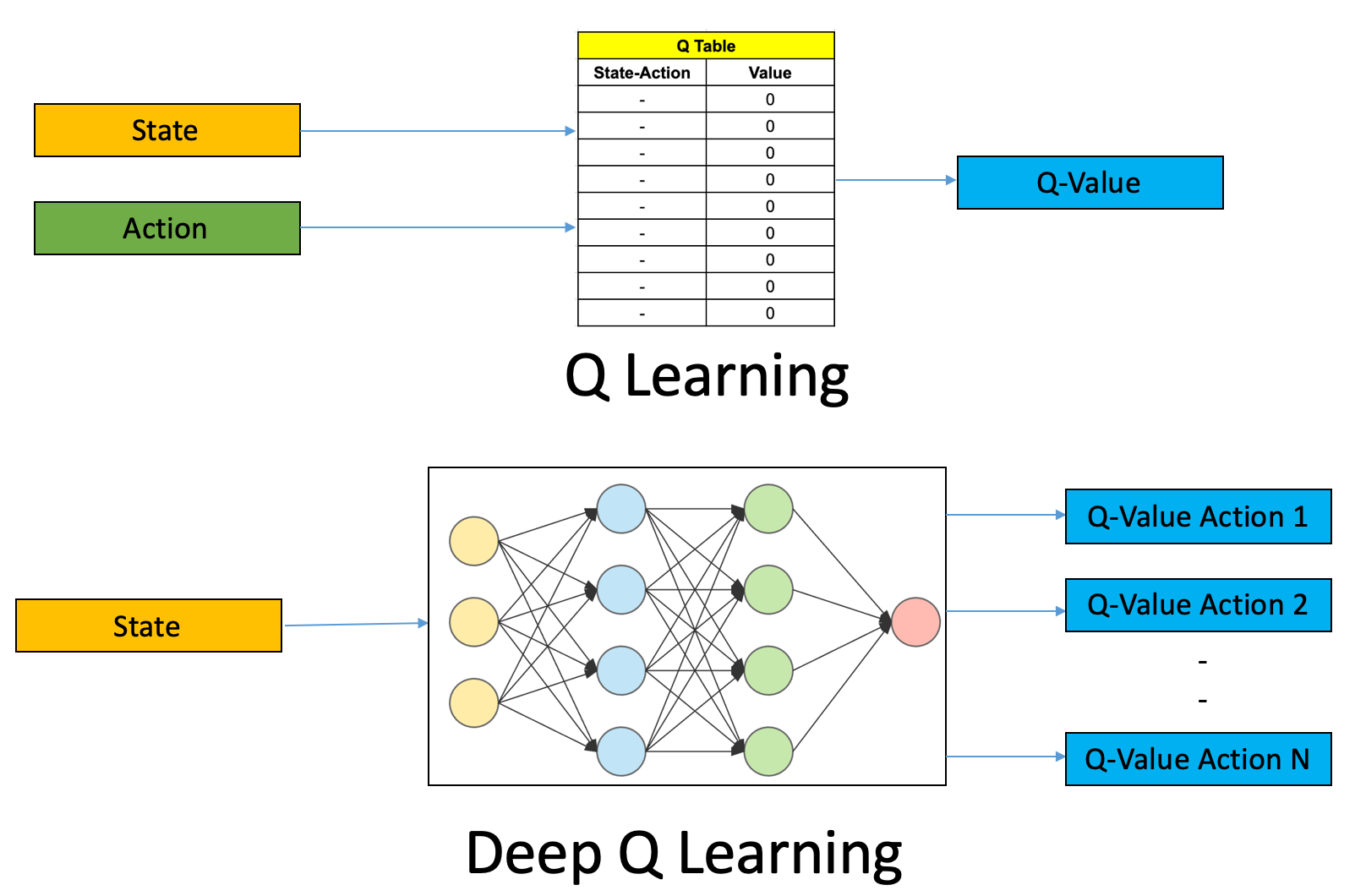Fig 1. Tabular Q-learning vs DQN.
(Image source: Ankit Choudhary.)
그러나, 딥러닝을 강화학습에 적용할 때 몇가지 문제가 있다:
- Delayed Rewards: 대부분의 딥러닝 문제들은 많은 양의 hand-labeled data를 사용하여 학습한다. 그러나 강화학습에서는 agent가 선택한 action에 대해 즉각적인 reward를 받지 않을 수 있으며, 이러한 reward는 sparse하거나 noisy하다.
- High Correlation: 연속적인 상태들은 서로 상관관계가 높을 수 있다. 이는 학습 데이터간의 i.i.d 가정을 깨뜨릴 수 있다.
- Non-stationary Distribution: 강화학습에서는 agent가 학습을 진행함에 따라 얻게 되는 data의 distribution이 변할 수 있다. 이는 fixed underlying distribution을 가정하는 딥러닝에서 문제가 될 수 있다.
DQN은 이러한 문제들을 해결하기 위해 다음과 같은 기법들을 사용한다:
- CNN(Convolutional Neural Networks): 이미지와 같은 high-dimensional raw data로부터 feature를 추출하기 위해 CNN을 사용한다.
- Experience Replay: agent가 경험한 데이터를 저장하고 이를 무작위로 뽑아서 학습한다. 이는 데이터간의 상관관계를 줄이고, 학습 데이터의 분포를 고정시킨다.
- Fixed Q-targets: target Q-value를 계산할 때 target network를 사용하여 target Q-value를 계산한다. 이는 학습 중 target Q-value를 고정시킴으로써 학습을 안정화시킨다.
DQN이 도입한 이러한 기법들은 후에 나오는 발전된 알고리즘들에도 많은 영향을 끼쳤다.
Objective
DQN은 action-value를 추정하는 Q-function을 학습한다. 구체적으로, action-value를 추정하는 Q-network $Q(s,a;\theta)$를 정의하고, 이를 학습하여 optimal action-value function $Q^*(s,a)$에 근접시킨다. 이때, $\theta$는 neural network의 parameter이다. 만약, 각 iteration $i$마다 Q-network에 대한 target value인 $y_i$가 존재한다면, Q-network를 학습하기 위한 loss function $L_i(\theta_i)$를 아래와 같이 정의할 수 있다:
\[L_i(\theta_i) = \mathbb{E}_{s,a \sim \rho(\cdot)} \left[ \left( y_i - Q(s,a;\theta_i) \right)^2 \right]\]그러나, 일반적으로 강화학습에서는 label이 존재하지 않기 때문에 target value인 $y_i$를 구성하기 어렵다. 이를 해결하기 위해 DQN은 target value를 temporal difference(TD) target으로 정의한다. TD target은 아래와 같이 정의된다:
\[y_i = \mathbb{E}_{s' \sim \mathcal{E}} \left[ r + \gamma \max_{a'} Q(s',a';\theta_{i-1}) \right \vert s,a]\]TD target의 주요한 의미는, 현재 state $s$에서 action $a$를 선택했을 때 얻게 되는 실제 데이터 reward $r$과 다음 state $s’$에서 최적의 action을 선택했을 때 얻게 되는 action-value의 추정치를 고려하여 현재 state에서의 action-value를 추정한다는 것이다. 이러한 loss function의 gradient는 아래와 같다:
\[\nabla_{\theta_i} L_i(\theta_i) = \mathbb{E}_{s,a \sim \rho(\cdot); s' \sim \mathcal{E}} \left[ \left( r + \gamma \max_{a'} Q(s',a';\theta_{i-1}) - Q(s,a;\theta_i) \right) \nabla_{\theta_i} Q(s,a;\theta_i) \right]\]몰론, 실제로는 위처럼 완전한 expectation을 계산하는 것이 아닌, stochastic gradient descent(SGD)를 사용하여 mini-batch를 통해 gradient를 추정한다.
이러한 알고리즘에는 주요한 특징이 있다:
- Model-free: DQN은 model-free 알고리즘이다. 즉, environment의 dynamics에 대한 정보를 알 필요가 없으며, sample로부터 직접적으로 학습한다.
- Off-policy: DQN은 off-policy 알고리즘이다. experience samples는 behavior policy (e.g., epsilon-greedy policy)로부터 수집되지만, agent는 target policy인 greedy policy $a = \arg \max_a Q(s,a;\theta)$를 학습한다.
Method
DQN의 핵심 component들은 아래와 같다:
- Q-Network: Q-network는 state $s$로부터 action들에 대해 Q-value를 추정하는 neural network이다.
- Target Network: Target network는 target Q-value를 계산하기 위한 neural network이다. Target network는 fixed interval로 Q-network의 parameter를 복사하여 업데이트한다. 이는 학습 중 target Q-value를 고정시킴으로써 학습을 안정화시킨다.
- Experience Replay: Experience replay는 experience tuple $(s,a,r,s’)$를 저장하고 이를 무작위로 뽑아서 학습하는 기법이다. 이는 데이터간의 상관관계를 줄인다.
아래는 DQN의 architecture이다:
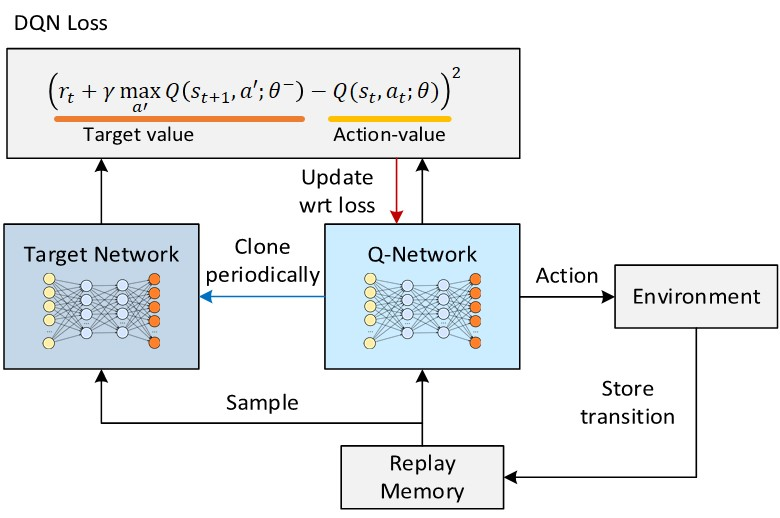Fig 2. DQN Architecture.
(Image source: 이것저것 테크블로그.)
agent는 매 time step $t$마다 environment 상호작용하면서 experience sample을 획득한 후 이를 replay buffer에 저장한다. 이후, replay buffer로부터 mini-batch를 뽑아서 Q-value를 학습한다. 이러한 과정을 통해 DQN은 optimal Q-value function에 근접하도록 학습된다. 아래는 DQN의 알고리즘이다:
Fig 3. DQN Algorithm.
(Image source: Playing Atari with Deep Reinforcement Learning.)
몰론, 위 알고리즘에서는 따로 target network에 대해 기술되어있지 않지만, TD target $y_j$를 계산할 때 target network를 사용한다. 또한, target network는 fixed interval로 Q-network의 parameter를 복사하여 업데이트한다.
Limitations
DQN은 분명 Atari 게임과 같은 high-dimensional state space이며 다루는데 효과적이었다. 그러나 DQN에는 몇가지 한계점이 있다:
- High-dimensional Action Space: DQN은 high-dimensional discrete action space나 continuous action space에는 적용하기 어렵다. 이는 Q-value를 추정하기 위해 discrete action space를 가정하기 때문이며, 모든 action에 대해 Q-value를 추정하기 때문이다.
- Off-policy: DQN은 off-policy method이기 때문에 sample-efficient하지만, 학습이 느리고 불안정할 수 있다.
후에 나오는 알고리즘들은 이러한 한계점을 극복하기 위해 다양한 기법들을 사용한다.
Summary
- deep neural network를 사용해 high-dimensional state space를 효과적으로 다룰 수 있다.
- experience replay와 target network를 사용하여 학습을 안정화시킨다.
- model-free, off-policy method이다.
- high-dimensional action space나 continuous action space에는 적용하기 어렵다.
References
[1] Mnih, Volodymyr, et al. “Playing atari with deep reinforcement learning.” arXiv preprint arXiv:1312.5602 (2013).