이 포스트에서는 요즘 가장 핫한 딥러닝 모델인 Transformer를 DQN에 적용한 Deep Transformer Q-Networks for Partially Observable Reinforcement Learning 논문에 대해 소개한다. 이 논문의 주 목적은 POMDP 상황에서 RNN 계열의 한계를 극복하고자 Transformer를 DQN에 적용한 것이다.
Partial Observability
강화학습에서 agent가 현재 state에 대한 모든 정보를 알고 있는 경우, 이를 fully observable MDP라고 한다. 그러나, 대부분의 실제 환경에서는 agent가 현재 state에 대한 모든 정보를 알 수 없는 경우가 많다. agent는 현재 state로부터 관찰된 일부 정보만을 가지고 의사결정을 해야하며, 이러한 상황을 partially observable markov decision process (POMDP)라고 한다. 아래는 POMDP environment인 Gym-Gridverse이다:
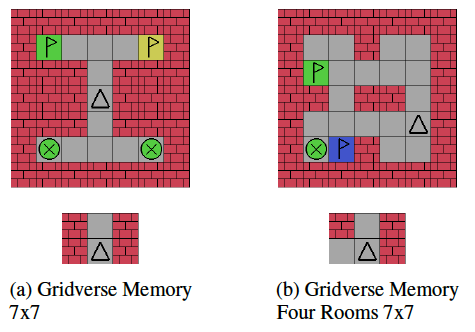Fig 1. POMDP: Gym-Gridverse.
(Image source: Deep Transformer Q-Networks for Partially Observable Reinforcement Learning.)
위 그림에서, 위쪽 행은 전체 state를 나타내는 그림이고, 아래쪽 행은 agent가 관찰할 수 있는 부분만을 나타낸 그림이다. agent는 X표시되어있는 beacon의 색깔과 동일한 깃발에 도달해야한다. 일반적인 MDP는 agent가 현재 state만을 가지고 action을 선택하는 markov property를 가정한다. 그러나, 위와 같은 환경에서는 agent가 현재 state에 대한 정보를 완전히 알지 못하기 때문에 학습에 어려움을 겪으며, 종종 실패한다. 따라서, 이러한 문제를 다루기 위한 방법이 필요하다.
Limitation of RNN
partial observability를 다루기 위해서는 RL agent는 이전의 observation들을 기억할 필요가 있다. RL에서는 memory component를 추가해 agent가 이전의 observation을 참조할 수 있도록 한다. 이러한 memory component로 recurrent neural network (RNN)이 많이 사용되었다. LSTM이나 GRU와 같은 RNN 계열의 방법들은 observation 혹은 action-observation history에 대한 sequence를 sequential하게 처리함으로써 POMDP 문제를 해결할 수 있었다. 그러나, RNN은 long-term dependency에 취약하다. 이는 RNN이 긴 sequence에 대한 정보를 잘 학습하지 못한다는 것을 의미한다. 이로 인해 RNN을 사용했다고 할 지라도, POMDP 문제에서 종종 학습에 실패하는 경우가 발생한다.
이는 RL만의 문제가 아니다. NLP 분야에서도 RNN의 한계가 논의되었고, 이를 극복하기 위해 Transformer가 제안되었다. Transformer는 self-attention mechanism을 사용하여 long-term dependency를 잘 학습할 수 있다. 따라서, Transformer를 RL에 적용하여 RNN의 한계를 극복하고자 한 것이 이 논문의 주 목적이다.
Related Work
몰론, RL에 Transformer를 적용한 연구는 이 논문이 처음이 아니다. 대표적으로 Decision Transformer 등이 있다. 그러나, 이전 연구들은 주로 offline RL setting이거나 supervised learning setting이었다. 반면, 이 논문에서 제안한 방법은 완전히 online RL setting이다. 나는 이 논문에서는 DQN을 사용했지만 다른 보다 강력한 RL 알고리즘에도 쉽게 적용할 수 있을 걸로 본다.
Deep Transformer Q-Networks
이제 본격적으로 이 논문에서 제안한 Deep Transformer Q-Networks (DTQN)에 대해 알아보자. DTQN은 DQN에 Transformer를 활용한 모델로 아래는 DTQN의 핵심 요소이다:
- Observation Embedding: 현재 observation을 포함한 observation history를 embedding한다. 이는 Transformer의 input으로 사용된다.
- Transformer Decoder: Transformer의 decoder를 사용하여 observation history sequence를 처리한다. 이는 각 action의 Q-value를 추정하는 데 사용된다.
- Q-value Prediction: 예측된 Q-value를 사용하여 action을 선택하고, TD error를 계산하여 네트워크를 학습한다.
아래는 DTQN의 architecture이다:
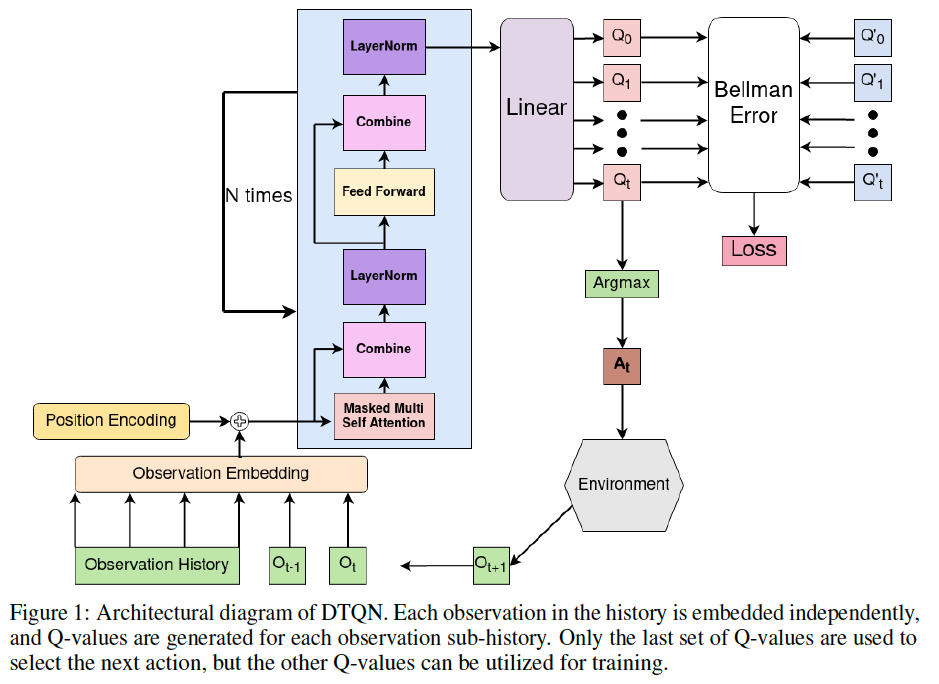Fig 2. DTQN Overall Architecture.
(Image source: Deep Transformer Q-Networks for Partially Observable Reinforcement Learning.)
이제 구체적으로 각 요소에 대해 알아보자.
Observation Embedding and Positional Encodings
agent의 최근 $k$개의 observation history $h_{t:t+k}$에서 각각의 observation은 observation embedding layer를 통해 transformer의 dimensionality로 linearly projected된다. 이후, learned positional encoding을 각 observation에 더해준다.
NLP task에서 positional encoding은 Transformer에 흔히 사용되는 방법으로, 주로 sinusoidal positional encoding이 사용된다. 이는 문장의 각 token의 위치에 대한 정보를 제공함으로써 Transformer가 sequence의 순서를 학습할 수 있도록 도와준다. 그러나 RL에서는 observation history에서 각 observation의 순서가 중요할 수도 있고 아닐수도 있다. 이는 task와 environment에 따라 다르다. 따라서, 이 논문에서는 positional encoding을 학습 가능한 parameter로 설정하여 observation history의 순서에 대한 정보를 학습하도록 한다. 아래는 각 domain에 따라 학습된 positional encoding과 sinusoidal positional encoding을 비교한 결과이다:
Fig 3. Positional Encoding Comparisons.
(Image source: Deep Transformer Q-Networks for Partially Observable Reinforcement Learning.)
Transformer Decoder
Transformer는 sequence data를 처리하는데 효과적임이 이미 널리 알려져있다. 특히, attention mechanism은 가장 중요한 token들에 더 많은 가중치 혹은 attention을 줌으로써 효과적으로 학습할 수 있다. Transformer는 encoder-decoder 구조로 되어있지만, 최근에는 주로 encoder (BERT)나 decoder (GPT)를 단독으로 사용한다. 두 방법의 주요한 차이점은 decoder는 attention layer에 causal masking을 적용하는 것이다. 즉, $i$번째 token은 $i$번째 이전의 token에만 attention을 줄 수 있다. 이는 decoder가 다음 token을 예측할 때, 이전 token들만을 참조할 수 있도록 한다. DTQN은 decoder만을 사용한다.
구체적으로 DTQN에서는 GPT와 같이 두개의 submodule로 구성된다: masked multi-headed self-attention과 position-wise feedforward network. 구체적으로는 다음 스텝을 따른다:
- 앞서 embedding된 observation history를 weight matrix $W^Q$에 의해 query $Q$, $W^K$에 의해 key $K$, $W^V$에 의해 value $V$로 projection한다.
- $Q$, $K$, $V$는 masked multi-headed self-attention을 거친 후, observation embedding과 combine된 후, layer normalization을 거친다.
- 이후, position-wise feedforward network를 거친 후, combine, layer normalization을 거친다.
- 이러한 과정을 $N$개의 Transformer block을 통해 $N$번 반복한다.
- 마지막 embedding은 action space로 projection되어 각 action에 대한 Q-value를 추정한다.
사실 이는 전형적인 Transformer의 구조이다.
Q-value Prediction
이후의 과정은 DQN과 거의 유사하다. 먼저, DQN은 Mean Squared Bellman Error를 minimize하도록 학습된다:
\[L(\theta) = \mathbb{E}_{(s,a,r,s') \sim \mathcal{D}} [ ( r + \gamma \max_{a' \in \mathcal{A}} Q(s',a';\theta') - Q(s,a;\theta) )^2 ]\]experience tuple $(s,a,r,s’)$는 replay buffer $\mathcal{D}$로부터 uniformly하게 샘플링된다. TD target $r + \max_{a’ \in \mathcal{A}} Q(s’,a’;\theta’)$는 $\theta’$으로 parameterized된 target network를 사용하여 계산된다. 이는 $\theta$에 의해 parameterized된 Q-network보다 지연되어 업데이트되기 때문에 학습을 안정화시킨다.
그러나 앞서 언급했듯이, partially observable 도메인에서는 네트워크의 입력을 state에서 observation으로 단순히 바꾸는 것만으로는 학습이 어렵다. 따라서, DTQN은 observation history를 Transformer로 처리하여 Q-value를 추정한다.
이때, DTQN은 observation history의 각 time step에 대한 모든 Q-value를 추정한다. agent가 action을 결정할 때에는 현재 time step $t$에 대한 Q-value만을 사용한다. 즉, 다시 말해 history의 마지막 time step에 대한 Q-value만을 사용한다. 그러나 학습할 때는 history 내의 모든 time step에 대한 Q-value를 사용한다. 몰론 마지막 time step에 대한 Q-value만을 사용하는 것이 직관적일 수 있지만 이는 매우 큰 낭비이다. 이는 실제로 모든 time step에 대한 Q-value를 사용했을 때 학습 성능이 크게 향상되었다.
Algorithm
아래는 DTQN의 알고리즘이다:
Fig 4. DTQN Algorithm.
(Image source: Deep Transformer Q-Networks for Partially Observable Reinforcement Learning.)
위 알고리즘에서 Q-value를 추정할 때 $s$가 아닌 $h_{t:t+i}$가 입력됨을 확인할 수 있다. 또한, loss를 계산할 때 casually-masked self-attention mechanism을 사용하기 때문에, 알고리즘에 묘사된 for loop는 실제로 one forward pass로 처리된다.
Experiments
이 논문에서는 DTQN을 다양한 POMDP 환경에서 평가하였으며, 다양한 ablation study를 진행하였다. 보다 자세한 결과와 해석은 논문을 직접 참고하기 바란다. 아래는 DTQN을 다른 방법과 비교한 결과이다 (파란색: DTQN, 주황색: DRQN, 갈색: DQN):
Fig 5. DTQN against Baselines.
(Image source: Deep Transformer Q-Networks for Partially Observable Reinforcement Learning.)
위 실험결과를 보면 알 수 있듯이 naive한 DQN은 POMDP 문제에서 학습에 실패하거나 어려움을 겪음을 알 수 있다. 이는 POMDP 문제를 해결하기 위해서는, memory component가 필요함을 보여준다. DRQN은 LSTM을 통해 DQN에 memory component를 추가한 것이다. DRQN은 분명 좋은 성능을 보이지만, 학습이 느리고 불안정함을 알 수 있다. 반면, DTQN은 빠른 학습 속도와 좋은 성능을 보인다.
아래는 ablation study 결과에 대한 표이다:
Fig 6. Ablations.
(Image source: Deep Transformer Q-Networks for Partially Observable Reinforcement Learning.)
먼저, DTQN에 learned position encoding을 사용했을 때 positional encoding을 사용하지 않았을 때보다 성능이 향상되었음을 알 수 있으며, sinusoidal positional encoding을 사용했을 때보다 약간 개선됨을 알 수 있다. 또한, 마지막 time step에 대한 Q-value만을 사용해 학습했을 때 성능이 매우 떨어짐을 확인할 수 있다.
Transformer의 이점 중 하나는 self-attention weight를 시각화 할 수 있는 것이다. 직관적으로, self-attention mechanism은 agent가 task를 해결하는데 가장 유용한 정보를 제공하는 observation에 더 많이 우선순위를 둘 것이다. 아래 그림은 Gridverse 환경에 대해 self-attention weight를 시각화한 결과이다:
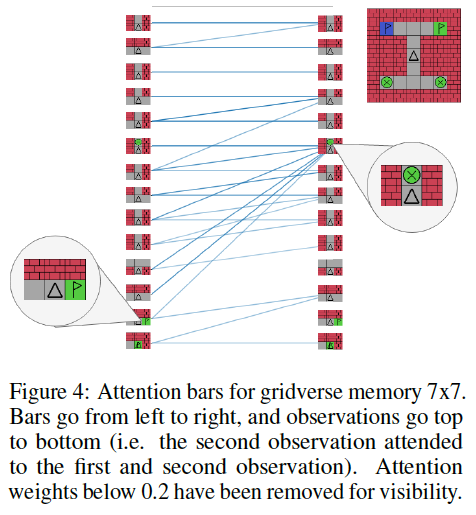Fig 7. Atttention Visualization.
(Image source: Deep Transformer Q-Networks for Partially Observable Reinforcement Learning.)
초록색 beacon을 포함하는 observation이 모든 future observations에 의해 attention을 받는 것을 확인할 수 있다. 이는 DTQN이 task를 해결하는데 어느 observation이 중요한지를 적절히 학습하고 있음을 나타낸다. agent가 초록색 flag를 볼 때 (위 그림에서 왼쪽), agent는 초록색 beacon에 attention을 주고, 올바른 flag임을 확실시 할 수 있다.
Summary
아래는 DTQN의 요약이다:
- DQN에 Transformer를 활용한 모델로, POMDP 문제를 해결하기 위해 제안되었다.
- fully online RL setting에서 사용할 수 있다.
- observation history를 Transformer decoder로 처리하여 Q-value를 추정한다.
- learned positional encoding을 사용한다.
- observation history의 추정된 모든 Q-value를 사용하여 학습한다.
- DQN과 DRQN에 비해 빠른 학습 속도와 좋은 성능을 보인다.
다만, 1가지 우려점이 존재한다. 원래, POMDP setting에서 observation history는 initial time step부터의 full history이다. 그러나, DTQN에서는 observation history가 context length $k$에 의해 truncated된다. 실제 실험에서 $k=50$으로 설정되었다. RNN은 이론상 full history를 처리한다. 그러나, DTQN은 truncated history이다. 만약, environment가 복잡하고 episode length가 매우 길때는 어떨지 궁금하다.
References
[1] Esslinger, Kevin, Robert Platt, and Christopher Amato. “Deep transformer q-networks for partially observable reinforcement learning.” arXiv preprint arXiv:2206.01078 (2022).