Dynamic Programming in RL

이 포스트에서는 RL에서 MDP로 environment의 perfect model이 주어졌을 때 optimal policy를 구하는데 사용되는 기초적인 방식인 Dynamic Programming (DP)를 소개한다.

Introduction

Reinforcement Learning (RL)에서 environment가 perfect model로 environment의 지식 (일반적으로 MDP)을 완전히 알 수 있다면 Dynamic Programming (DP)를 활용해 optimal policy를 계산할 수 있다. 즉, 모든 가능한 transition의 probability distribution을 완전히 알고 있어야 한다. 이는 굉장히 특수한 상황이다. 우리는 보통 어떤 state에서 action을 선택해 next state로의 transition이 발생했을 때 next state로 transition되었다는 결과만 안다. next state가 얼마나 존재하고 각 next state로 transition될 확률이 어느정도인지 알지 못한다. 이때는 sampling으로 획득한 environment에 대한 experience를 통해 RL 문제를 해결한다.

그렇다면 DP란 무엇일까? DP는 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 최적화 기법이다. DP는 일반적으로 아래와 같은 2가지 유형의 문제에 적용된다.

1. Overlapping Subproblems
2. Optimal Substructure

Overlapping Subproblems는 동일한 sub problem들이 반복적으로 요구될 때 연산 결과를 저장했다가 사용할 수 있음을 의미한다. Optimal Substructure은 주어진 문제를 sub problem들로 쪼갠 뒤 각각의 sub problem들의 최적해를 사용하여 원래 문제의 최적해를 구할 수 있음을 의미한다.

RL에 적용되는 DP의 핵심 아이디어는 위 2가지 특성을 모두 반영해 Bellman equation을 update rule로 전환하는 것이다. 이를 통해 value function을 근사시켜 RL 문제를 해결할 수 있다. 이 과정이 어떻게 진행되는지 알아보자.

Generalized Policy Iteration

Generalized Policy Iteration (GPI)는 RL 문제를 풀 때 사용되는 일반적인 접근 방법이다. GPI에는 다음과 같은 2가지 과정이 존재한다.

1. Policy Evaluation - policy $\pi$를 따를 때 value function $v_\pi$를 계산
2. Policy Improvement - 계산된 현재 value function을 통해 policy $\pi$를 개선

위 policy evaluation과 policy improvement는 번갈아 가며 수행된다. 아래 다이어그램을 보면 조금 더 직관적으로 이해할 수 있다.

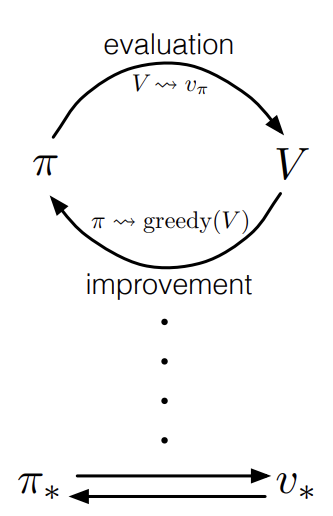Fig 1. GPI diagram.
(Image source: Sec. 4.6 Sutton & Barto (2018).)

policy evaluation과 policy improvement는 서로 경쟁하면서 협력하는 관계로 볼 수 있다. 이 둘은 서로를 반대 방향으로 잡아 당긴다. policy evaluation에서는 현재 policy $\pi$에 관해 value function $v_\pi$가 계산된다. 즉, value function을 policy 쪽으로 끌어당긴 셈이다. 반대로 policy improvement에서는 value function $v_\pi$에 관해 policy $\pi$가 개선되기 때문에 policy를 value function 쪽으로 끌어 당겼다. 이렇게 서로 끌어당기다 보면 어느 시점에 한 지점에 도달하게 되고 이 때가 바로 optimal value function과 policy이다. 이러한 관계를 나타내는 그림은 아래와 같다.

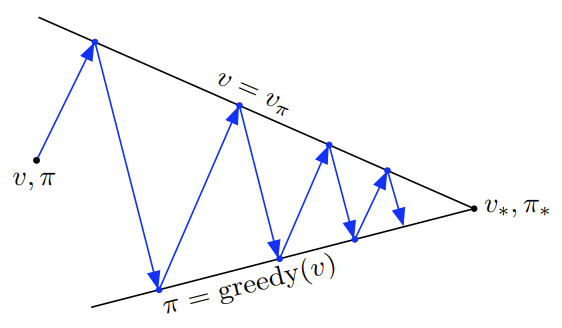Fig 2. GPI relationship.
(Image source: Sec. 4.6 Sutton & Barto (2018).)

몰론 실제로는 엄청나게 복잡한 과정이 내부에서 발생하지만 직관적으로 위와 같이 GPI를 이해할 수 있다. GPI에 대해 알아보았으니 이제 DP에서 GPI가 어떻게 적용되는지 알아보자.

Policy Evaluation (Prediction)

DP에서의 policy evaluation에 대해 알아보자. policy evaluation은 prediction으로 불리기도 한다. 먼저 Bellman equation을 리마인드하자.

\[\begin{align} v_\pi(s) &\doteq \mathbb{E}_\pi[R_{t+1} + \gamma v_\pi(S_{t+1}) \ \vert \ S_t = s] \\ &= \sum_a\pi(a \vert s) \sum_{s',r}p(s',r \vert s,a) \Big[r + \gamma v_\pi(s') \Big] \tag{1} \end{align}\]

DP에서는 위 Bellman equation을 아래와 같은 연속적인 update rule로 적용해 value function $v(s)$를 풀 수 있다.

\[\begin{align} v_{k+1}(s) &\doteq \mathbb{E}_\pi[R_{t+1} + \gamma v_k(S_{t+1}) \ \vert \ S_t = s] \\ &= \sum_a\pi(a \vert s) \sum_{s',r}p(s',r \vert s,a) \Big[r + \gamma v_\pi(s') \Big] \tag{2} \end{align}\]

DP에서는 위 update rule이 모든 state $s \in \mathcal{S}$에 대해 수행되며 $v_k$는 일반적으로 $k \rightarrow \infty$이면 수렴한다. 이 때 terminal state의 value는 항상 0이어야 한다. 이렇게 iterative하게 value function을 구하는 알고리즘을 iterative policy evaluation이라고 부른다.

iterative policy evaluation이 DP인 이유는 update rule을 수행하는 방식 때문이다. 기존 Bellman equation (1)을 Exhaustive search를 통해 푼다고 생각해보자. 현재 state $s$의 value $v_\pi(s)$는 transition된 next state $s’$의 $v_\pi(s’)$으로부터 계산된다. $v_\pi(s’)$은 다시 transition된 s’의 후속 state $s’‘$의 $v_\pi(s’’)$로부터 계산된다. 즉, 재귀적 관계로 연속된 모든 후속 MDP를 고려해야하는 굉장히 비효율적인 방식이다.

DP에서는 기존 Bellman equation을 update rule로 전환해 iterative하게 만들었다. 이때 연속된 모든 후속 state를 관찰하는게 아니라 현재 state $s$에서 가능한 next state들에 대한 one-step transition만을 고려한다. 현재 state의 new value $v_{k+1}(s)$는 후속 state $s’$의 old value $v_k(s’)$로부터 계산되며 다시 재귀적으로 계산하지 않고 지금까지 계산된 $v_k(s’)$을 그대로 사용하겠다는 것이다. 즉, optimal policy를 찾기 위해 각 state별로 쪼개 optimal state value를 구하며 이때 지금까지 구한 state value를 저장해 놓았다가 다음 iteration에서 연산 시 사용하기 때문에 DP의 2가지 특성을 모두 지니고 있다. 아래 그림을 보자.

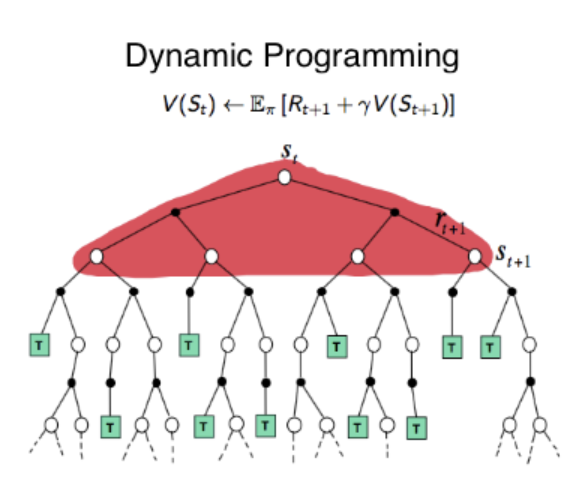Fig 3. DP backup diagram.
(Image source: Robotic Sea Bass. An Intuitive Guide to Reinforcement Learning.)

위 그림은 DP의 backup diagram으로 어떤 과정을 거쳐 state value $v_{k+1}(s)$가 계산되는지를 보여준다. 이때 흰색 원은 state, 검은색 원은 action이다. Exhaustive search로 Bellman equation을 푼다면 위 backup diagram의 아래 모든 후속 state들을 고려해야 한다. 그러나 DP에서는 현재 state에서의 one-step transition만을 고려하기 때문에 위 backup diagram에 표시된 빨간색 영역만을 고려한다.

iterative policy evaluation의 각 iteration은 모든 state에 대해 한번에 이러한 update rule을 수행한다. 따라서 iterative policy evaluation을 수행하기 위해서는 일반적으로 old value를 저장한 array와 new value를 계산하기 위한 array가 각각 필요하다. 그러나 실제로는 한개의 array로 old value의 보관과 new value의 계산을 동시에 수행한다. 이때는 new value가 계산되면 기존 old value를 실시간으로 덮어쓴다. 따라서 각 state에 대한 value 계산 시 old value가 참조될 수도 있고, 이미 계산이 완료된 new value가 참조될 수도 있다. 2-array든 1-array 방식이든 수렴성은 보장되며 1-array 방식이 수렴속도가 일반적으로 더 빠르다. 다만 1-array 방식은 state value를 update하는 순서에 따라 수렴 속도가 변한다.

지금까지 DP를 통해 state value $v_\pi$를 계산하는 방법을 알아보았다. 이제 계산된 state value를 통해 policy $\pi$를 개선해보자.

Policy Improvement

임의의 deterministic policy $\pi$를 따를 때의 state value $v_\pi$가 결정되었다고 가정하자. deterministic policy의 의미는 policy $\pi$의 결과가 action들의 확률 분포가 아닌 action 그 자체인 경우를 말한다. 이 때 어떻게 기존 policy를 개선할 수 있을까? 이는 action value $q_\pi$를 통해 수행할 수 있다. 먼저 action value $q_\pi$를 remind 하자.

\[\begin{align} q_\pi(s,a) &\doteq \mathbb{E}[R_{t+1} + \gamma v_\pi(S_{t+1}) \ \vert \ S_t = s, A_t = a] \\ &= \sum_{s',r}p(s',r \vert s,a)\Big[r + \gamma v_\pi(s') \Big] \tag{3} \end{align}\]

모든 state $s \in \mathcal{S}$에 대해 action value가 아래와 같은 관계를 만족한다고 하자.

\[q_\pi(s, \pi'(s)) \geq v_\pi(s) \tag{4}\]

이 경우 모든 state로부터 아래와 같이 더 많거나 같은 expected return을 얻을 수 있다.

\[v_\pi'(s) \geq v_\pi(s) \tag{5}\]

이를 policy improvement theorem이라고 한다. 그렇다면 어떻게 수식 (4)를 만족할 수 있을까? 가장 간단한 방법은 각 state에서 action value $q_\pi(s,a)$가 최대인 action을 선택하는 것이다. $v_\pi(s)$는 action value들의 expectation이다. 따라서 최대 action value보다 작거나 같다. 이러한 방식을 greedy policy라고 하며 new policy $\pi’$은 아래와 같다.

\[\pi'(s) \doteq \underset{a}{\arg\max} \ q_\pi(s, a) \tag{6}\]

개선된 정책 $\pi’(s)$는 기존 $\pi(s)$에 의한 action과 같을 수도 있고 다를 수도 있지만 무엇이든 간에 분명히 기존 policy만큼 좋거나 더 나을것이다. 기존 policy에 의한 value function에 관해 greedy하게 선택하는 과정을 policy improvement라고 한다.

만약 new greedy policy $\pi’$이 기존 policy $\pi$와 동일하면 어떨까? 이 경우 기존 policy와 동일한 action을 선택하기 때문에 모든 state에 대해 $v_\pi = v_{\pi’}$이 되며 수식 (6)에 의해 아래와 같은 수식을 만족한다.

\[v_{\pi'}(s) = \max_a \mathbb{E}[R_{t+1} + \gamma v_{\pi'}(S_{t+1}) \ \vert \ S_t = s, A_t = a] \tag{7}\]

그런데 위 수식은 Bellman optimality equation과 동일하다. 따라서 $v_{\pi’}$은 $v_\ast$이며 $\pi$와 $\pi’$ 모두 optimal policy이다.

Policy Iteration

policy iteration은 policy evaluation과 policy improvement를 번갈아 수행하는 방법이다. 어떤 policy $\pi$를 평가해 $v_\pi$를 구한 뒤 이를 바탕으로 더 나은 policy $\pi’$를 얻는다. 다시 $\pi’$을 평가해 $v_{\pi’}$을 구한 뒤 이를 바탕으로 더 나은 policy $\pi’‘$를 얻는다. 이러한 과정을 반복하는 것이 바로 policy iteration이다. 아래는 policy iteration을 sequence 형태이다.

\[\pi_0 \overset{E}{\longrightarrow} v_{\pi_0} \overset{I}{\longrightarrow} \pi_1 \overset{E}{\longrightarrow} v_{\pi_1} \overset{I}{\longrightarrow} \pi_2 \overset{E}{\longrightarrow} \cdots \overset{I}{\longrightarrow} \pi_\ast \overset{E}{\longrightarrow} v_\ast\]

위 수식에서 $\overset{E}{\longrightarrow}$는 policy evaluation, $\overset{I}{\longrightarrow}$는 policy improvement를 나타낸다. finite MDP는 유한하기 때문에 이러한 프로세스는 유한한 iteration 안에 optimal policy와 optimal value function으로 반드시 수렴한다.

아래는 policy iteration 알고리즘이다.

$\text{Algorithm: Policy Iteration (using iterative policy evaluation) for estimating } \pi \approx \pi_\ast$

\(\begin{align*} & \textstyle \text{1. Initialization} \\ & \textstyle \qquad V(s) \in \mathbb{R} \text{ and } \pi(s) \in \mathcal{A}(s) \text{ arbitrarily for all } s \in \mathcal{S} \\ \\ & \textstyle \text{2. Policy Evaluation} \\ & \textstyle \qquad \text{Loop:} \\ & \textstyle \qquad\qquad \Delta \leftarrow 0 \\ & \textstyle \qquad\qquad \text{Loop for each } s \in \mathcal{S} \text{:} \\ & \textstyle \qquad\qquad\qquad v \leftarrow V(s) \\ & \textstyle \qquad\qquad\qquad V(s) \leftarrow \sum_{s',r}p(s',r \vert s, \pi(s))[r + \gamma V(s')] \\ & \textstyle \qquad\qquad\qquad \Delta \leftarrow \max(\Delta, \vert v - V(s) \vert) \\ & \textstyle \qquad \text{until } \Delta < \theta \text{ (a small positive number determining the accuracy of estimation)} \\ \\ & \textstyle \text{3. Policy Improvement} \\ & \textstyle \qquad \textit{policy-stable} \leftarrow \textit{true} \\ & \textstyle \qquad \text{For each } s \in \mathcal{S} \text{:} \\ & \textstyle \qquad\qquad \textit{old-action} \leftarrow \pi(s) \\ & \textstyle \qquad\qquad \pi(s) \leftarrow \arg\max_a \sum_{s',r}p(s',r \vert s,a)[r + \gamma V(s')] \\ & \textstyle \qquad\qquad \text{If } \textit{old-action} \neq \pi(s),\text{ then } \textit{policy-stable} \leftarrow \textit{false} \\ & \textstyle \qquad \text{If } \textit{policy-stable} \text{, then stop and return } V \approx v_\ast \text{ and } \pi \approx \pi_\ast; \text{ else go to 2} \end{align*}\)

참고로 2. Policy Evaluation에서 state value $V(s)$를 구할 때와 3. Policy Improvement에서 개선된 policy $\pi(s)$를 얻기 위해 action value를 구할 때의 수식이 동일한데 그 이유는 policy $\pi$를 deterministic 하다고 가정했기 때문이다. state value를 구할 때 policy $\pi$를 따를 때의 action value $q_\pi(s, a)$에 대한 expectation을 취하는데 policy $\pi$를 따르는 action $a$의 확률은 1, 나머지 action은 모두 0이기 때문에 $a = \pi(s)$에 대한 action value $q_\pi(s, \pi(s))$가 곧 state value이다.

Value Iteration

policy iteration은 policy evaluation을 통해 현재 policy에 대한 value function을 수렴시키고 나서 policy improvement를 수행할 수 있었다. 그러나 value iteration 기법은 policy evaluation을 수행 시 현재 policy에 대한 value function을 수렴시키지 않는다. 대신 현재 policy에 대한 value function을 딱 한 번만 계산 후 바로 policy improvement를 수행한다. 즉, policy evaluation의 1 iteration과 policy improvement를 결합한 것을 반복해서 수행한다. 이 과정을 하나의 단순한 update rule로 나타낼 수 있다.

\[\begin{align} v_{k+1}(s) &\doteq \max_a\mathbb{E}[R_{t+1} + \gamma v_k(S_{t+1}) \ \vert \ S_t = s, A_t = a] \\ &= \max_a \sum_{s',r}p(s',r \vert s,a) \Big[r + \gamma v_k(s') \Big] \tag{8} \end{align}\]

위 수식처럼 나타낼 수 있는 이유는 policy improvement시 action value가 최대인 action으로 policy가 개선되기 때문이다. 즉, greedy policy이기 때문에 다음 policy evaluation에서 action value가 최대인 action을 제외한 나머지 action이 policy에 의해 선택될 확률은 0다. 따라서 한 번의 update에서 action value의 max값을 선택하는 것과 동일해진다.

또한 위 수식 (8)은 Bellman optimality equation과 동일하다. 즉, Bellman optimality equation을 iterative한 update rule로 변경한 것이 value iteration이다. value iteration 역시 $k \rightarrow \infty$이면 $v_\ast$로 수렴하며 이때의 greedy policy가 곧 $\pi_\ast$이다.

아래는 value iteration 알고리즘이다.

$\text{Algorithm: Value Iteration, for estimating } \pi \approx \pi_\ast$

\(\begin{align*} & \textstyle \text{Algorithm parameter: a small threshold } \theta > 0 \text{ determining accuracy of estimation} \\ & \textstyle \text{Initialize } V(s) \text{, for all } s \in \mathcal{S}^+ \text{, arbitrarily except that } V(\textit{terminal}) = 0 \\ \\ & \textstyle \text{Loop:} \\ & \textstyle \qquad \Delta \leftarrow 0 \\ & \textstyle \qquad \text{Loop for each } s \in \mathcal{S} \text{:} \\ & \textstyle \qquad\qquad v \leftarrow V(s) \\ & \textstyle \qquad\qquad V(s) \leftarrow \max_a \sum_{s',r}p(s',r \vert s,a)[r + \gamma V(s')] \\ & \textstyle \qquad\qquad \Delta \leftarrow \max(\Delta, \vert v - V(s) \vert) \\ & \textstyle \text{until } \Delta < \theta \\ \\ & \textstyle \text{Output a deterministic policy, } \pi \approx \pi_\ast \text{, such that} \\ & \textstyle \qquad \pi(s) = \arg\max_a \sum_{s',r}p(s',r \vert s,a)[r + \gamma V(s')] \end{align*}\)

지금까지 value iteration에 대해 알아보았다.

Summary

이번 포스트에서는 finite MDPs를 풀기 위해 dynamic programming 기법을 활용한 방법을 알아보았다. policy evaluation은 주어진 policy에 대한 value function을 계산한다. policy improvement는 계산된 value function을 바탕으로 policy를 개선한다. DP에서의 policy iteration은 policy evaluation과 policy improvement를 번갈아 수행한다. 반면 value iteration은 policy evaluation의 1 iteration과 policy improvement를 결합한 방식을 수행한다. 이때 policy iteration은 Bellman expected equation, value iteration은 Bellman optimality equation이 사용된다는 차이가 있다. DP에서의 이러한 과정은 generalized policy iteration (GPI)로 나타낼 수 있으며 이는 대부분의 reinforcement learning (RL)에도 적용된다. 따라서 RL에서의 DP를 이해하는 것은 중요하다고 볼 수 있다.

References

[1] Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction; 2nd Edition. 2018.
[2] Towards Data Science. Rohan Jagtap. Dynamic Programming in RL.