Eligibility Traces

이번 포스트에서는 TD와 Monte Carlo method를 통합 및 일반화하는 eligibility traces에 대해 다룰 것이다.

Introduction

eligibility traces는 TD와 Monte Carlo (MC) method를 통합 및 일반화하는 방법으로 스펙트럼에 걸쳐 있다. 스펙트럼의 양 끝에는 MC method ($\lambda=1$)와 1-step TD method ($\lambda=0$)가 있다. 또한 eligibility traces는 MC method를 online 학습과 continuing task에서의 학습을 가능하게 한다.

eligibility traces와 비슷한 방법으로 $n$-step TD method가 존재한다.¹ 그러나 eligibility traces는 $n$-step TD method보다 우아한 알고리즘적 메커니즘을 지니고, 상당한 계산적 이점을 가진다.

eligibility traces는 단기 기억 vector인 eligibility trace $\mathbf{z}_t \in \mathbb{R}^d$와 동시에 장기 기억 weight vector $\mathbf{w}_t \in \mathbb{R}^d$를 사용한다. 이 둘이 무슨 역할을 하는 지 곧 알아볼 것이다.

eligibility traces가 $n$-step method에 비해 가지는 주요한 계산적 이점은 마지막 $n$개의 feature vector를 저장하는 대신, 단 하나의 trace vector만을 사용한다는 것에서 비롯된다. 또한 $n$-step method는 $n-1$ time step만큼 학습이 지연되고 episode 종료를 포착해야하는 반면, eligibility traces는 학습이 지속적이고 균일하게 수행된다.

MC method와 $n$-step method는 각각 모든 미래 reward와 $n$개의 reward에 기반해 업데이트가 수행된다. 이렇게 업데이트되는 state로부터 앞 혹은 미래를 바라보는 것에 기반하는 방법을 forward view라고 부른다. 그러나 eligibility trace를 사용할 경우, 업데이트되는 state로부터 최근 방문했던 state를 향해 뒤 혹은 과거를 바라보는데, 이러한 방법을 backward view라고 한다.

이 내용들을 이제 차근차근 알아볼 것이다. 평소처럼 먼저 state value에 대한 prediction을 알아본 뒤, action value와 control로 확장한다.

The $\lambda$-return

먼저, $n$-step return에 대해 리뷰를 하자. $n$-step return $G_{t:t+n}$은 아래와 같이 $n$개의 discounted reward와 $n$-step에 도달된 state의 discounted 추정치를 더한 값으로 정의된다.

\[G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1}R_{t+n} + \gamma^n\hat{v}(S_{t+n}, \mathbf{w}_{t+n-1}), \quad 0 \leq t \leq T - n\]

$\hat{v}(s,\mathbf{w})$는 weight vector $\mathbf{w}$가 주어졌을 때 state $s$에서의 추정치이다. $T$는 episode의 terminal time step이며 $n \geq 1$이다.

우리의 이번 목적인 $\lambda$-return은 모든 $n$에 대한 $n$-step return들의 평균으로 TD($\lambda$) 알고리즘에 사용된다. 각 가중치는 $\lambda^{n-1} \text{ (where $\lambda \in [0, 1)$)}$에 비례하며, 가중치의 총합을 1로 설정하기 위해 $1 - \lambda$에 의해 정규화된다. 아래는 $\lambda$-return의 정의이다.

\[G_t^\lambda \doteq (1 - \lambda) \sum_{n=1}^\infty \lambda^{n-1}G_{t:t+n}\]

위 수식을 아래와 같이 episode 종료 전후로 분리할 수 있다.

\[G_t^\lambda = (1 - \lambda)\sum_{n=1}^{T-t-1} \lambda^{n-1}G_{t:t+n} + \lambda^{T-t-1}G_t\]

이 수식은 $\lambda = 1$일 때의 상황을 더 명확히 해준다. $\lambda = 1$일 때 왼쪽 main sum은 0이 되며 기본적인 return $G_t$만 남게 된다. 따라서 $\lambda = 1$일 때 $\lambda$-return은 MC method이다. 반대로 $\lambda = 0$일 때 오직 one-step return $G_{t:t+1}$만 남게 되기 때문에 one-step TD method이다. $\lambda$-return은 $n$-step return과 비교했을 때 MC method와 one-step TD method 사이를 조금 더 부드럽게 이동할 수 있다. 아래는 $\lambda$-return에서 $n$-step return sequence에 가중치를 부여하는 것을 나타낸 backup diagram이다.

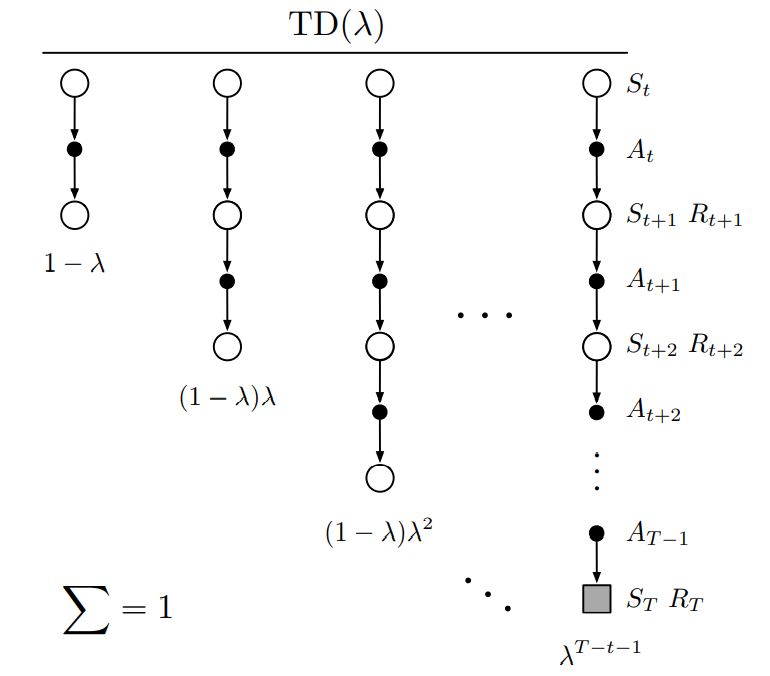Fig 1. The backup diagram for TD($\lambda$).
(Image source: Sec 12.1 Sutton & Barto (2020).)

아래는 각 $n$-step return에 부여되는 가중치의 변화 추이를 나타내는 그림이다. terminal time step 이후의 $n$-step return은 실제 return $G_t$이다.

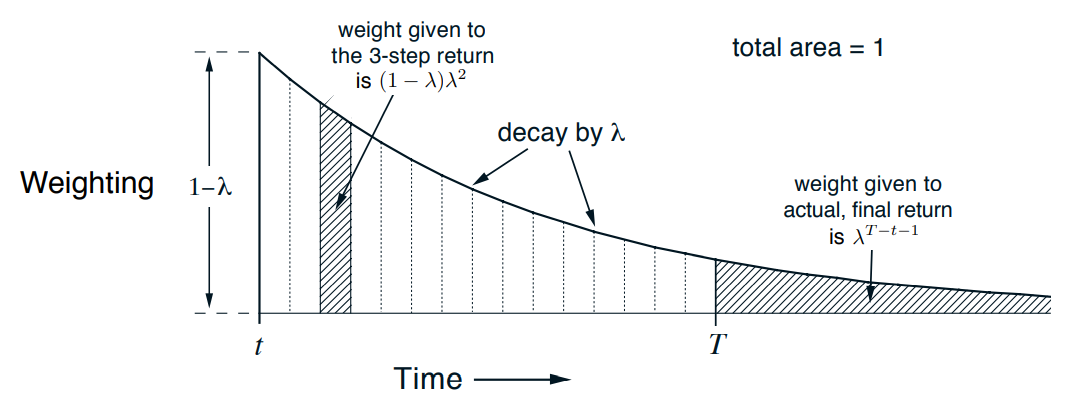Fig 2. Weighting given in the $\lambda$-return to each of the $n$-step returns.
(Image source: Sec 12.1 Sutton & Barto (2020).)

이제 $\lambda$-return에 기반한 첫번째 알고리즘을 정의하자. 굉장히 naive한 알고리즘으로 off-line $\lambda$-return algorithm이라고 부른다. off-line 알고리즘인 이유는 episode 동안 weight vector가 변하지 않기 때문이다. episode 종료 후에, 전체 off-line update sequence가 아래 일반적인 semi-gradient rule을 따라 수행된다. 이 때 target은 $\lambda$-return $G_t^\lambda$이다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \Big[G_t^\lambda - \hat{v}(S_t, \mathbf{w}_t) \Big] \nabla \hat{v}(S_t, \mathbf{w}_t), \quad t = 0, \dots, T - 1\]

그렇다면 왜 episode 종료까지 기다려야 할까? 이유는 비교적 간단하다. $n$-step TD method는 $n$-step return을 계산하기 위해 $n$번의 transition이 발생할 때까지 기다려야 했다. $\lambda$-return은 기본적으로 $G_{t:t+1}$부터 $G_t$까지 모든 return을 포함한다. $G_t$를 계산하기 위해서는 episode 종료를 기다려야만 한다.

우리가 지금까지 알아본 방법은 forward view이다. time step $t$에서 어떤 state $S_t$를 update할 때 우리는 $t+1, t+2, \dots$와 같이 미래의 보상과 state를 본다. 이 state를 업데이트한 후 다음 state로 넘어가면, 우리는 이전 state를 결코 다시 보지 않는다. 반대로 미래의 것들은 반복적으로 처리된다. 아래는 이러한 forward view의 관계를 나타내는 그림이다.

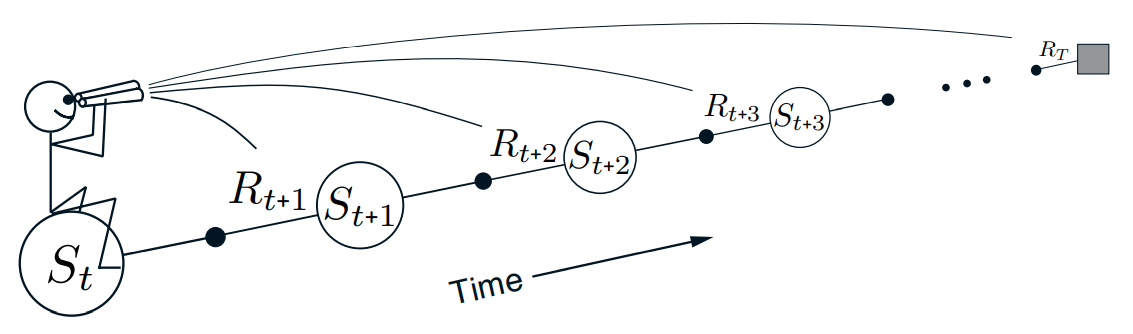Fig 3. The forward view.
(Image source: Sec 12.1 Sutton & Barto (2020).)

TD($\lambda$)

TD($\lambda$)는 off-line $\lambda$-return을 아래와 같이 3가지 방식으로 개선하였다.

1. episode의 모든 step에서 weight vector를 업데이트할 수 있음
2. 1의 이유로 계산이 동등하게 분배됨
3. 1의 이유로 continuing problem에 적용 가능

eligibility trace는 vector $\mathbf{z}_t \in \mathbb{R}^d$는 weight vector $\mathbf{w}_t$와 동일한 차원이다. weight vector는 시스템의 lifetime 동안 누적되는 장기기억인 반면, eligibility trace는 한 episode 길이보다 적게 지속되는 단기기억이다. 이러한 eligibility trace는 weigh vector에 영향을 미친다.

TD($\lambda$)에서 eligibility trace vector는 episode 시작 시에 zero vector로 초기화되며 아래와 같이 업데이트 된다.

\[\begin{align*} & \mathbf{z}_{-1} \doteq \mathbf{0}, \\ & \mathbf{z}_t \doteq \gamma \lambda \mathbf{z}_{t-1} + \nabla \hat{v}(S_t, \mathbf{w}_t), \quad 0 \leq t \leq T \end{align*}\]

$\lambda$는 이전 section에서 소개된 parameter로 이제 trace-decay parameter로 부를 것이다. eligibility trace는 weight vector의 각 원소가 최근 state value에 어떻게 기여하는지를 추적한다. 여기서 “최근”은 $\gamma\lambda$에 의해 정의된다.

이제 eligibility trace를 사용해 weight vector를 업데이트하는 방법을 살펴보자. 먼저, state value에 대한 TD error는 아래와 같다.

\[\delta_t \doteq R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w}_t) - \hat{v}(S_t, \mathbf{w}_t)\]

TD($\lambda$)에서 weight vector는 scalar TD error와 vector eligibility trace에 비례하여 업데이트 된다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \delta_t \mathbf{z}_t\]

아래는 알고리즘이다.

$\text{Algorithm: Semi-gradient TD($\lambda$) for estimating $\hat{v} \approx v_\pi$}$

\(\begin{align*} & \textstyle \text{Input: the policy $\pi$ to be evaluated} \\ & \textstyle \text{Input: a differentiable function $\hat{v} : \mathcal{S}^+ \times \mathbb{R}^d \rightarrow \mathbb{R}$ such that $\hat{v}(\text{terminal}, \cdot) = 0$} \\ & \textstyle \text{Algorithm parameters: step size $\alpha > 0$, trace decay rate $\lambda \in [0,1]$} \\ & \textstyle \text{Initialize value-function weights $\mathbf{w}$ arbitrarily (e.g., $\mathbf{w} = \mathbf{0}$)} \\ \\ & \textstyle \text{Loop for each episode:} \\ & \textstyle \qquad \text{Initialize $S$} \\ & \textstyle \qquad \mathbf{z} \leftarrow \mathbf{0} \qquad \text{(a $d$-dimensional vector)} \\ & \textstyle \qquad \text{Loop for each step of episode:} \\ & \textstyle \qquad\qquad \text{Choose } A \sim \pi(\cdot \vert S) \\ & \textstyle \qquad\qquad \text{Take action $A$, observe $R, S'$} \\ & \textstyle \qquad\qquad \mathbf{z} \leftarrow \gamma \lambda \mathbf{z} + \nabla \hat{v}(S, \mathbf{w}) \\ & \textstyle \qquad\qquad \delta \leftarrow R + \gamma \hat{v}(S', \mathbf{w}) - \hat{v}(S, \mathbf{w}) \\ & \textstyle \qquad\qquad \mathbf{w} \leftarrow \mathbf{w} + \alpha \delta \mathbf{z} \\ & \textstyle \qquad\qquad S \leftarrow S' \\ & \textstyle \qquad \text{until $S'$ is terminal} \\ \end{align*}\)

TD($\lambda$)는 시간을 거꾸로 향한다. $\lambda$에 의해 현재 time step으로부터 시간적으로 더 멀리 떨어진 이전 state일 수록 더 적게 update된다. 더 멀리 떨어질 수록 더 많이 discount되기 때문이다. 즉, 더 이전의 state에게 TD error에 대한 더 낮은 신용을 준다. 아래는 이에 대한 그림이다.

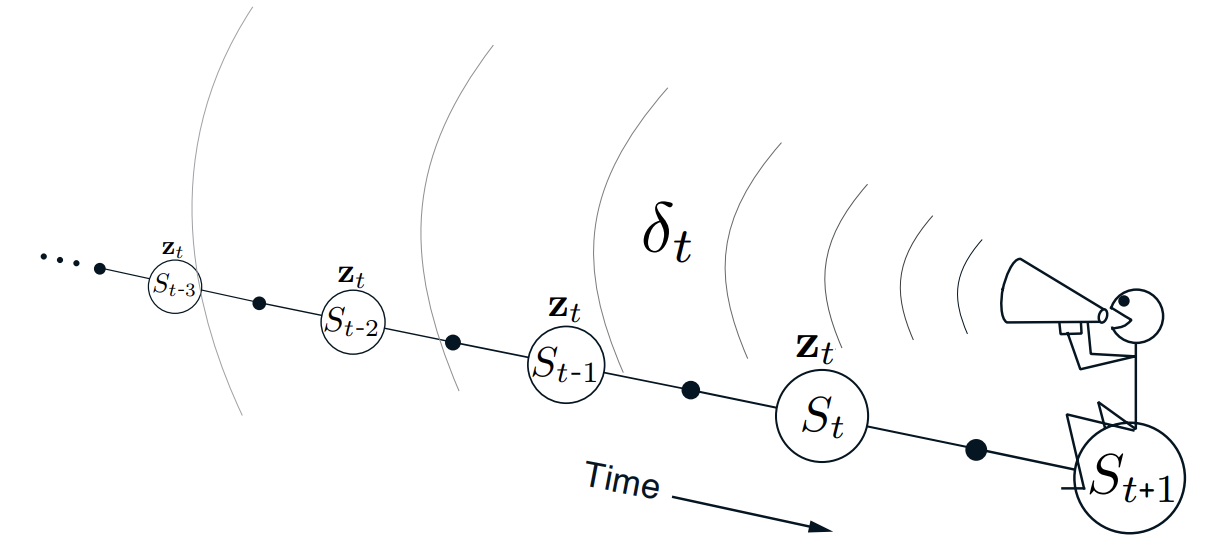Fig 4. The backward view.
(Image source: Sec 12.2 Sutton & Barto (2020).)

$\lambda = 0$일 때 $\mathbf{z}_t = \nabla\hat{v}(S_t, \mathbf{w}_t)$로 TD($\lambda$)의 update는 one-step semi-gradient TD update가 된다. 이를 TD(0)라 부른다. 반대로 $\lambda$가 1일 때는 신용은 오직 $\gamma$에 의해서만 감소한다. 이는 결국 MC method로 여길 수 있다. 이를 TD(1)이라고 부른다. 그러나 TD(1)은 MC method와 다르게 continuing task에도 적용할 수 있으며, online으로 학습할 수 있다.

$n$-step Truncated $\lambda$-return Methods

앞서 봤던 off-line $\lambda$-return 알고리즘을 개선시켜보자. $\lambda$-return의 근본적인 문제는 episode 종료 전까지 실제 return $G_t$를 모른다는 것이다. 우리는 이 문제에 대해 이미 수없이 다뤄왔다. 실제 return $G_t$를 bootstrapping을 통해 근사화하면 된다. 데이터가 이후 horizon $h$까지 주어졌을 때, $\lambda$-return을 아래와 같이 변경할 것이며 이를 truncated $\lambda$-return이라고 한다.

\[G_{t:h}^\lambda \doteq (1 - \lambda) \sum_{n=1}^{h-t-1} \lambda^{n-1} G_{t:t+n} + \lambda^{h-t-1}G_{t:h}, \quad 0 \leq t < h \leq T\]

기존 $\lambda$-return에서 terminal time step $T$가 horizon $h$로 대체되었으며, 실제 return $G_t$가 $n$-step return $G_{t:h}$로 대체되었다. 기존 $n$-step method에서는 $n$-step return만 사용했지만 여기서는 $1 \leq k \leq n$에 대해 모든 $k$-step return이 포함된다. truncated $\lambda$-return을 사용한 TD update를 Truncated TD($\lambda$) (TTD($\lambda$))라고 하며 아래는 이에 대한 backup diagram이다.

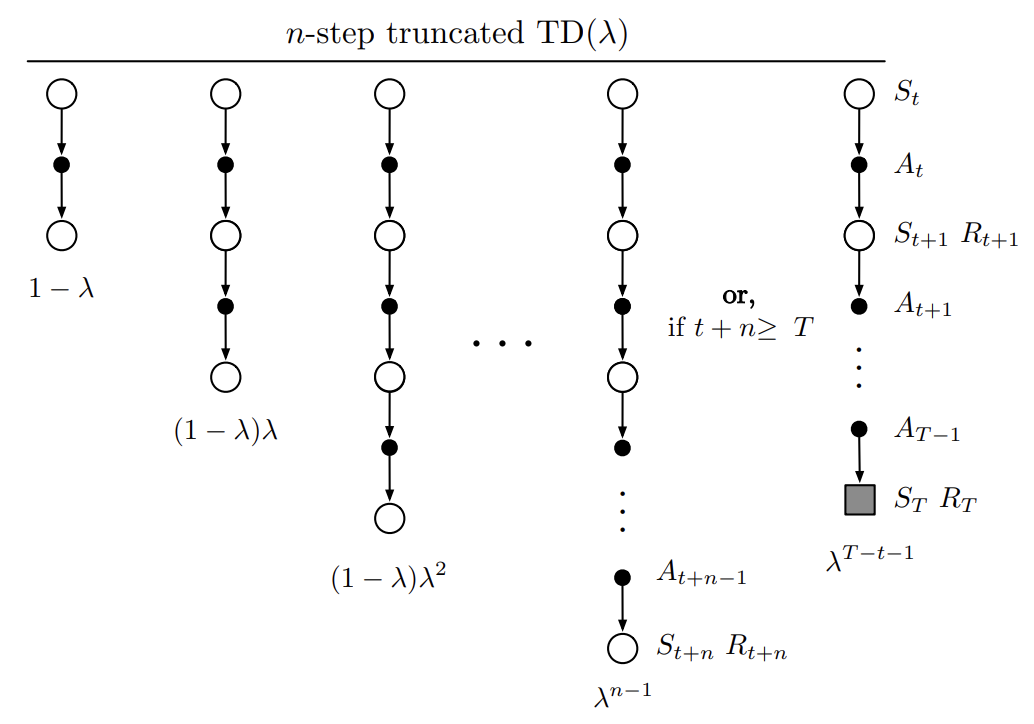Fig 5. The backup diagram for Truncated TD($\lambda$).
(Image source: Sec 12.3 Sutton & Barto (2020).)

기존 TD($\lambda$)와 비교했을 때 TTD($\lambda$)는 가장 긴 요소가 episode 종료가 아닌, 최대 $n$-step까지 diagram이 이어진다. TTD($\lambda$)는 아래와 같이 정의된다.

\[\mathbf{w}_{t+n} \doteq \mathbf{w}_{t+n-1} + \alpha \big[G_{t:t+n}^\lambda - \hat{v}(S_t, \mathbf{w}_{t+n-1}) \big] \nabla\hat{v}(S_t, \mathbf{w}_{t+n-1}), \quad 0 \leq t < T\]

Sarsa($\lambda$)

이제 action-value method로 확장하자. off-line $\lambda$-return algorithm의 action-value 형식은 단순히 $\hat{v}$을 $\hat{q}$으로 대체하기만 하면 된다.

\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \Big[G_t^\lambda - \hat{q}(S_t,A_t,\mathbf{w}_t) \Big] \nabla \hat{q}(S_t,A_t,\mathbf{w}_t), \quad t = 0,\dots,T-1\]

$G_t^\lambda \doteq G_{t:\infty}^\lambda$이다.

action value에 대한 TD method는 이러한 forward view를 근사화한다. 이를 Sarsa($\lambda$)라고 하며 TD($\lambda$)와 동일한 update rule을 가진다.

\[\begin{align*} & \mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \delta_t \mathbf{z}_t, \\ & \delta_t \doteq R_{t+1} + \gamma \hat{q}(S_{t+1},A_{t+1},\mathbf{w}_t) - \hat{q}(S_t,A_t,\mathbf{w}_t), \\ & \mathbf{z}_{-1} \doteq \mathbf{0}, \\ & \mathbf{z_t} \doteq \gamma \lambda \mathbf{z}_{t-1} + \nabla \hat{q}(S_t,A_t,\mathbf{w}_t), \quad 0 \leq t \leq T \end{align*}\]

아래는 Sarsa($\lambda$)의 backup diagram이다.

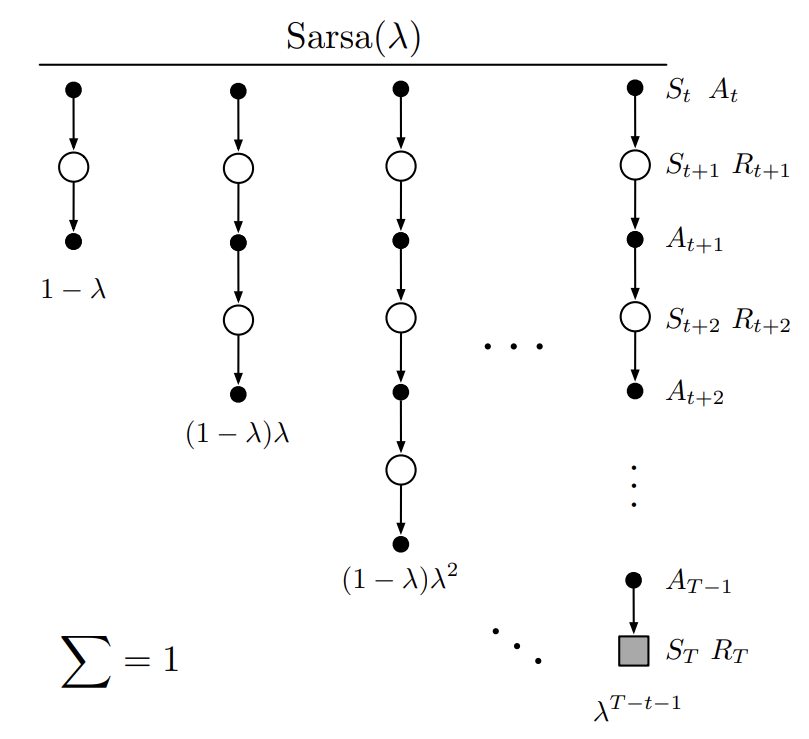Fig 6. Sarsa($\lambda$)’s backup diagram.
(Image source: Sec 12.7 Sutton & Barto (2020).)

아래는 그동안 알아보았던 Sarsa를 비교하는 좋은 그림이다. 왜 eligibility trace가 one-step과 $n$-step method보다도 상당히 효율적인지 알 수 있다.

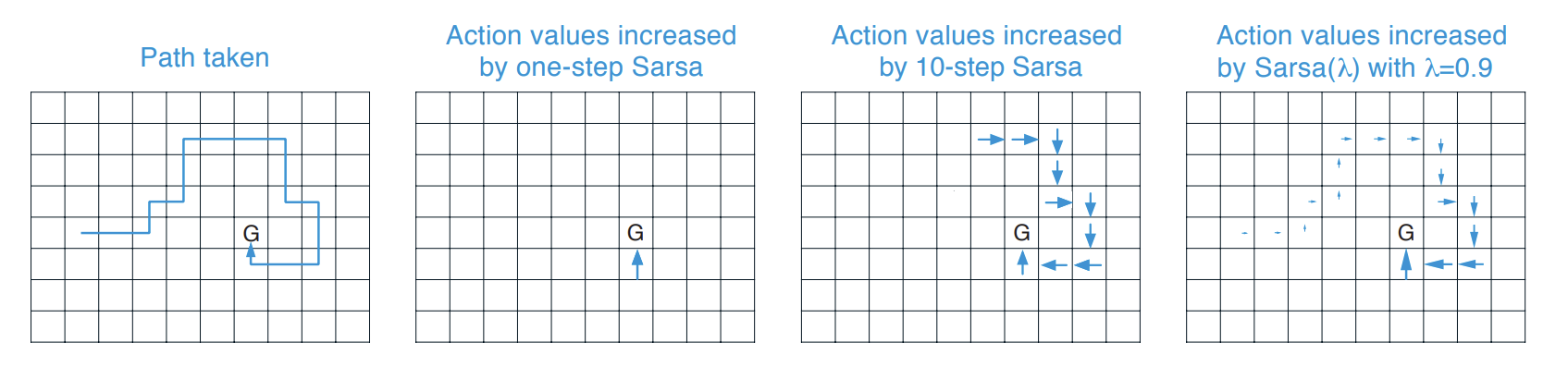Fig 7. Comparison of control algorithms in Gridworld.
(Image source: Sec 12.7 Sutton & Barto (2020).)

eligibility trace method는 episode의 시작까지 모든 action value를 업데이트 하지만 최근으로부터 멀리 떨어질 수록 더 적은 정도로 업데이트한다. 가장 매력적이고 종종 가장 강력한 방법이다.

Summary

• $\lambda$-return은 $n$-step return의 모든 $n$에 대한 평균으로 더 일반화된 형식
• weight vector는 장기 기억, eligibility trace vector는 단기 기억
• TD($\lambda$)는 backward view로 이전 state들을 추적
• eligibility trace는 episode의 시작까지 모든 value를 최근성에 따라 다른 정도로 업데이트

References

[1] Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction; 2nd Edition. 2020.

Footnotes

1. DevSlem. n-step Bootstrapping.. ↩