이 포스트에서는 Reinforcement Learning에서 기반이 되는 finite Markov Decision Processes (MDPs)와 finite MDPs 문제를 해결하기 위한 Bellman equations에 대해 소개한다.
What is MDPs
Markov Decision Processes (MDPs)는 연속적인 의사 결정을 형식화한 프레임이다. MDPs와 Multi-armed bandits 환경의 가장 큰 차이점은 MDPs에서는 선택한 action들이 environment의 states를 변경시켜 future rewards에 영향을 미친다는 점이다. 즉, actions와 states가 연관성이 있는 associative setting이다. MDPs는 $(\mathcal{S}, \mathcal{A}, P, R)$로 구성되며 각 요소는 아래와 같다.
- $\mathcal{S}$ - a set of states
- $\mathcal{A}$ - a set of actions
- $P$ - state-transition probability function
- $R$ - reward function
MDPs에서는 앞서 말했듯이 actions가 immediate rewards 뿐만 아니라 이후의 states들과 future rewards에 영향을 미친다. 그렇기 때문에 MDPs에서는 immediate rewards와 future rewards 사이에 tradeoff를 할 필요가 있다.
MDPs에서 learner이자 decision maker를 agent라고 하며, agent가 상호작용하는 agent 외의 모든 요소를 environment라고 한다. decision making은 agent가 action을 선택하는 행위이다. discrete time steps $t = 0, 1, 2, 3, \dots$이 있을 때 각 time step $t$에서 agent는 environment의 state $S_t \in \mathcal{S}$에서 action $A_t \in \mathcal{A}(s)$를 선택한다. 그러면 새로운 state $S_{t+1}$로 전이되고 environment로부터 numerical reward $R_{t+1} \in \mathcal{R} \subset \mathbb{R}$을 획득한다. 아래는 MDP에 대한 그림이다.
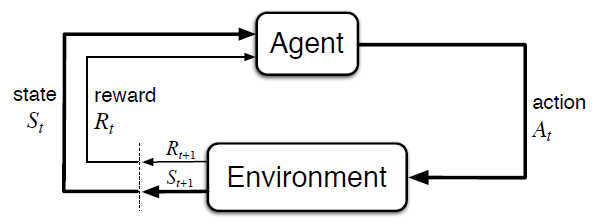Fig 1. The agent–environment interaction in a Markov decision process.
(Image source: Sec. 3.1 Sutton & Barto (2018).)
위 과정은 매 time step 마다 끊임없이 반복되며 MDP와 agent는 아래와 같은 sequence 혹은 trajectory를 생성한다.
\[S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, R_3, \dots\]이러한 states, actions, rewards ($\mathcal{S}$, $\mathcal{A}$, $\mathcal{R}$) 모두 유한할 때 finite MDP라고 한다. 이 때 $R_t$와 $S_t$는 잘 정의된 discrete probability distribution으로 이전의 모든 state나 action들이 아닌 오직 직전 state $S_{t-1}$과 action $A_{t-1}$에만 의존하며 $S_{t-1}$과 $A_{t-1}$이 주어졌을 때 $S_t$와 $R_t$가 발생할 확률 $p$를 정의할 수 있다.
\[p(s', r \vert s, a) \doteq \text{Pr}\lbrace S_t = s', R_t = r \ \vert \ S_{t-1} = s, A_{t-1} = a \rbrace\]위 function $p$는 MDP의 dynamics를 정의한다. state는 미래에 대한 차이를 만들어내는 과거의 agent-environment interaction에 대한 모든 측면의 정보를 포함해야하며, 이 때 state는 Markov property를 가진다고 말한다.
위에서 정의한 dynamics $p$로부터 state-transition probability를 유도할 수 있다.
\[p(s' \vert s, a) \doteq \text{Pr}\lbrace S_t = s' \ \vert \ S_{t-1} = s, A_{t-1} = a \rbrace = \sum_{r \in \mathcal{R}}p(s', r \vert s, a)\]또한 state-action pair에 대한 expected reward를 계산할 수 있다.
\[r(s, a) \doteq \mathbb{E}[R_t \ \vert \ S_{t-1} = s, A_{t-1} = a] = \sum_{r \in \mathcal{R}}r\sum_{s' \in \mathcal{S}}p(s', r \vert s, a)\]state-action-next-state에 대한 expected reward 역시 계산할 수 있다.
\[r(s, a, s') \doteq \mathbb{E}[R_t \ \vert \ S_{t-1} = s, A_{t-1} = a, S_t = s'] = \sum_{r \in \mathcal{R}}r\dfrac{p(s', r \vert s, a)}{p(s' \vert s, a)}\]이 포스트에서는 위 수식 중 dynamics $p(s’, r \vert s, a)$를 주로 사용하였다.
Goals in RL
Reinforcement Learning (RL)에서 agent는 immediate reward가 아닌 오랜 기간에 걸친 cumulative reward를 maximize하는 것을 목표로 한다. reward는 우리가 달성하고자 하는 것을 나타내는 중요한 지표이다. 주의할 점은 이 reward signal을 설정할 때 how가 아닌 what의 관점으로 설정해야한다. 달성하고자 하는 목표가 무엇인지에 초점을 맞추되 이것을 달성하기 위한 지식을 제시해서는 안된다.
Episode
배틀그라운드라는 게임을 생각해보자. 이 게임은 배틀로얄 장르로 매치 시작 시 비행기에서 낙하 후 총기를 비롯한 아이템을 파밍해 전투를 펼치는 게임이다. 각 매치는 싱글플레이 기준 매치 도중 사망하거나 적이 전부 사망해 홀로 생존 시 종료되며 다시 매치 시작 시 이전 매치에서 획득한 총기, 아이템 등은 전부 초기화된다. 각 매치는 사망 혹은 홀로 생존과 같이 terminal state가 존재하는데 게임 내 모든 상호작용을 하나의 sequence라고 볼 때 매치 단위의 subsequence로 쪼갤 수 있다. 이러한 subsequence를 episode라고 하는데 episode는 앞서 언급한 terminal state에 종료된다. terminal state는 주로 게임에서의 승리나 패배와 같다. episode가 terminal state에 도달해 종료되면 다시 처음 state로 초기화되고 새로운 episode가 시작된다. 새로운 episode는 이전 episode와 독립적인 관계이다. 이러한 종류의 episodes를 가진 tasks를 episodic tasks라고 부른다.
Return
cumulative reward를 수학적으로 정의한 것이 expected return $G_t$이며 이는 time step $t$ 이후에 획득한 rewards sequence $R_{t+1}, R_{t+2}, R_{t+3}, \dots ,$에 대한 함수이다. $G_t$를 구할 때 단순히 rewards sequence의 합으로 구할 수 있지만 이는 episodic tasks에서만 유효하다. terminal state가 존재하지 않는 continuing tasks에서는 무한한 time steps에서 rewards를 획득하기 때문에 $G_t \rightarrow \infty$가 될 것이다. 따라서 episodic tasks 뿐만 아니라 continuing tasks에서도 expected return $G_t$를 구하기 위해 일반적으로 미래가 고려된 discounted rewards sequence의 합으로 구한다. 이를 discounted return이라고 하며 수식은 아래와 같다.
\[G_t \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots = \sum_{k=t+1}^T \gamma^{k-t-1}R_k\]$T$는 termination time으로 continuing task면 $T = \infty$이다. $0 \leq \gamma \leq 1$는 discount rate로 더 먼 미래에 획득한 reward일수록 더 많이 discount한다.
위 수식을 연속적인 time steps에서의 return 형태로 변경할 수 있다. 즉, 재귀적으로 변경할 수 있는데 이는 강화학습 전반에서 굉장히 중요한 수식이다.
\[\begin{aligned} G_t &\doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \gamma^3 R_{t+4} \cdots \\ &= R_{t+1} + \gamma(R_{t+2} + \gamma R_{t+3} + \gamma^2 R_{t+4} \cdots) \\ &= R_{t+1} + \gamma G_{t+1} \end{aligned}\]Value Function
value function은 states 혹은 state-action pairs가 얼마나 좋은지를 추정하는 함수이다. “얼마나 좋은가”는 보통 expected return의 관점에서 정의된다. 미래에 획득할 rewards는 agent가 행동하는 방식에 의존하기 때문에 이에 대한 value functions는 agent의 행동 방식인 policy에 영향을 받는다. policy는 각 state에서 가능한 각 행동들의 선택 확률로 agent가 time step $t$에서 policy $\pi$를 따를 때, $\pi(a \vert s)$는 $S_t = s$일 때 $A_t = a$일 확률이다.
agent가 state $s$에 있을 때 agent에게 얼마나 좋은지를 추정하는 state-value function $v_\pi(s)$는 state $s$에서 시작하고 policy $\pi$를 따를 때 얻을 수 있는 expected return이다. MDPs에서는 $v_\pi$를 아래와 같이 정의할 수 있다.
\[v_\pi(s) \doteq \mathbb{E}_\pi[G_t \ \vert \ S_t = s]\]주의할 점은 terminal state의 value는 항상 0이다.
위와 비슷하게 policy $\pi$에 대한 action-value function $q_\pi$는 state $s$에서 policy $\pi$에 따라 action $a$를 선택했을 때 얻을 수 있는 expected return이다.
\[q_\pi(s, a) \doteq \mathbb{E}_\pi[G_t \ \vert \ S_t = s, A_t = a]\]value function $v_\pi$와 $q_\pi$는 경험으로부터 추정된다. 경험이란 agent가 직접 states에 방문해보고 actions를 선택함으로써 얻게 되는 return과 같은 정보들을 말한다.
Bellman Expectation Equation
state-value function은 expected return $G_t \doteq R_{t+1} + \gamma G_{t+1}$와 같이 재귀적 관계를 만족한다. 즉, $v_\pi$를 현재 state value와 후속 state value 사이의 관계로 나타낼 수 있으며 이를 $v_\pi$에 대한 Bellman expectation equation이라고 한다. 수식은 아래와 같으며 복잡한 증명은 생략한다.
\[\begin{aligned} v_\pi(s) &\doteq \mathbb{E}_\pi[G_t \ \vert \ S_t = s] \\ & = \mathbb{E}_\pi[R_{t+1} + \gamma v_\pi(S_{t+1}) \ \vert \ S_t = s] \end{aligned}\]action-value function 역시 위와 마찬가지로 재귀적 관계를 나타내는 $q_\pi$에 대한 Bellman expectation equation으로 나타낼 수 있다.
\[q_\pi(s, a) \doteq \mathbb{E}_\pi[R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}) \ \vert \ S_t = s, A_t = a]\]$v_\pi$에 대한 Bellman expectation equation을 아래와 같은 backup diagram으로 나타낼 수 있다. 참고로 backup diagram인 이유는 후속 states에서의 value로부터 역으로 현재 state에서의 value를 구하는 backup operation 관계를 표현하고 있기 때문이다.
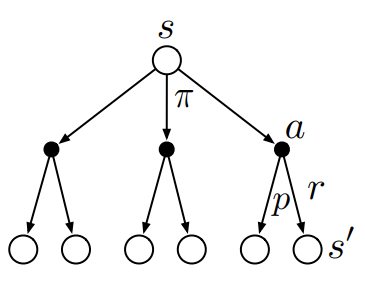Fig 2. Backup diagram for state-value.
(Image source: Sec. 3.5 Sutton & Barto (2018).)
비어있는 circle은 $v_\pi$, 검은색 circle은 $q_\pi$를 나타낸다. 가장 위의 node는 $v_\pi(s)$로 바로 아래의 $q_\pi(s, a)$를 가리킨다. 즉, $v_\pi$에 대한 Bellman expectation equation은 어떤 state에서 선택 가능한 각 action들의 action-value $q_\pi$들에 대한 expectation이다. 따라서 $v_\pi$를 아래와 같은 수식으로 나타낼 수 있다.
\[v_\pi(s) \doteq \sum_a\pi(a \vert s)q_\pi(s, a)\]$q_\pi$에 대한 Bellman expectation equation의 backup diagram은 아래와 같다.
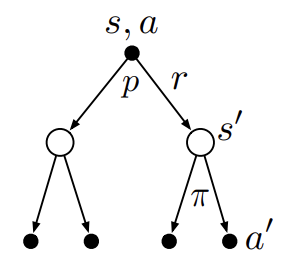Fig 3. Backup diagram for action-value.
(Image source: Sec. 3.5 Sutton & Barto (2018).)
$p$는 MDP의 dynamics로 state $s$에서 action $a$를 선택했을 때 reward $r$과 next state $s’$이 발생할 확률이다. 가장 위의 node는 $q_\pi(s, a)$로 바로 아래의 $v_\pi(s’)$을 가리킨다. 즉, $q_\pi(s, a)$는 어떤 state $s$에서 action $a$를 선택했을 때 획득한 return들의 expectation으로 나타낼 수 있다.
\[q_\pi(s, a) \doteq \sum_{s', r} p(s', r \vert s, a) \Big[r + \gamma v_\pi(s') \Big]\]위 두 Bellman expectation equation을 바탕으로 $v_\pi$를 아래와 같이 정의할 수 있다.
\[v_\pi(s) \doteq \sum_a \pi(a \vert s) \sum_{s', r}p(s', r \vert s, a)\Big[r + \gamma v_\pi(s') \Big]\]지금까지 알아본 내용은 특정 policy $\pi$를 따를 때 value를 추정하는 방법이다. 그러나 이것은 MDP에서 할 수 있는 최적의 방식이 아니다. 어디까지나 특정 policy $\pi$에 대한 value 추정일 뿐이다. 이제 MDP의 문제를 해결하는 방법을 알아보자.
Optimal Value Function
RL은 cumulative reward를 maximize하는 것이 목표로 한다. 위 Bellman equation의 수식을 보면 policy $\pi$에 따라 expected return을 나타내는 state value가 달라짐을 알 수 있다. 즉, cumulative reward는 policy $\pi$에 의존한다. 따라서 cumulative reward를 maximize하는 optimal policy $\pi_\ast$를 찾는 것이 목적이며 state-value function이 optimal policy를 따를 때 optimal state-value function $v_\ast$라 한다. 이때 $v_\ast$는 모든 policy에 대해 가장 큰 state-value function이다.
\[v_\ast(s) \doteq \max_\pi v_\pi(s)\]state-value는 expected return을 나타내기 때문에 optimal policy $\pi_\ast$를 따르는 optimal state-value 역시 maximize된다.
위와 마찬가지로 optimal action-value function $q_\ast$는 모든 policy에 대해 가장 큰 action-value function이다.
\[q_\ast(s, a) \doteq \max_\pi q_\pi(s, a)\]Optimal policy
그렇다면 optimal policy $\pi_\ast$를 어떻게 찾을 수 있을까? 어떤 한 policy $\pi$와 다른 policy $\pi’$이 있다고 할 때 모든 states에 대한 $\pi$를 따르는 value function이 모든 states에 대한 $\pi’$을 따르는 value function보다 크거나 같을 때 더 좋은 policy라고 판단할 수 있다. 이를 수식으로 나타내면 아래와 같다.
\[\pi \geq \pi' \ \text{if} \ v_\pi(s) \geq v_{\pi'}(s) \ \text{for all} \ s \in \mathcal{S}\]Bellman Optimality Equation
Bellman optimality equation은 Bellman expectation equation과 비슷하나 value들에 대한 expectation이 아닌 maximum value만을 고려한다는 차이가 있다. 아래는 optimal state-value function $v_\ast$에 대한 backup diagram이다.
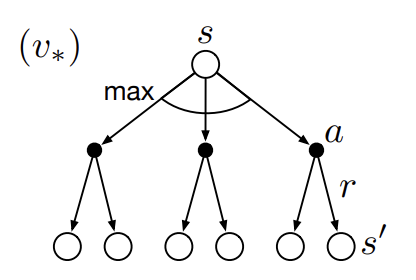Fig 4. Backup diagram for optimal state-value.
(Image source: Sec. 3.6 Sutton & Barto (2018).)
가장 위의 node $v_\ast(s)$는 action-value에 대해 maximum value를 선택한다. 즉, $v_\ast$에 대한 Bellman optimality equation은 optimal policy를 따르는 state value가 그 state에서의 best action에 대한 expected return 혹은 action value와 동일하다.
\[\begin{aligned} v_\ast(s) &= \max_{a \in \mathcal{A}(s)} q_{\pi_\ast}(s, a) \\ \end{aligned}\]아래는 optimal action-value function function $q_\ast$에 대한 backup diagram이다.
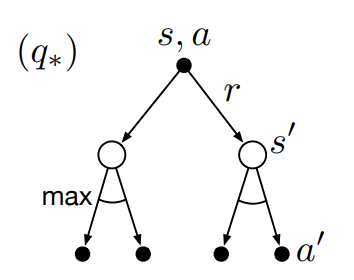Fig 5. Backup diagram for optimal action-value.
(Image source: Sec. 3.6 Sutton & Barto (2018).)
가장 위의 node는 $q_\ast(s, a)$로 바로 아래의 $v_\ast(s’)$을 가리킨다. $q_\ast$에 대한 Bellman optimality equation은 Bellman expectation equation과 같이 여전히 기댓값을 취하지만 유일한 차이점은 이미 각 states에 대한 optimal values를 알고 있다는 점이다.
\[q_\ast(s, a) \doteq \mathbb{E}[R_{t+1} + \gamma v_\ast(S_{t+1}) \ \vert \ S_t = s, A_t = a]\]위 내용을 바탕으로 $v_\ast$와 $q_\ast$에 대한 Bellman optimality equation을 다시 정의할 수 있다. 아래는 $v_\ast$에 대한 Bellman optimality equation을 현재 state와 후속 state 사이의 재귀적 관계로 표현한 수식이다.
\[\begin{aligned} v_\ast(s) &= \max_a \mathbb{E}[R_{t+1} + \gamma v_\ast(S_{t+1}) \ \vert \ S_t = s, A_t = a] \\ &= \max_a \sum_{s', r}p(s', r \vert s, a)\Big[r + \gamma v_\ast(s') \Big] \end{aligned}\]마찬가지로 $q_\ast$에 대한 Bellman optimality equation 역시 현재 state-action pair와 후속 state-action pair 사이의 재귀적 관계로 표현할 수 있다.
\[\begin{aligned} q_\ast(s, a) &= \mathbb{E} \Big[R_{t+1} + \gamma \max_{a'} q_\ast(S_{t+1}, a') \ \Big\vert \ S_t = s, A_t = a \Big] \\ &= \sum_{s', r}p(s', r \vert s, a) \Big[r + \gamma \max_{a'}q_\ast(s', a') \Big] \end{aligned}\]Bellman optimality equation을 풀면 RL의 목적인 optimal policy를 찾을 수 있다. 그러나 이 방법은 실제로 유용하지 않다. Bellman optimality equation을 푸는 행위는 exhaustive search와 유사한 행위이다. RL에서는 environment의 가능한 states가 계산이 불가능한 영역 수준으로 많다. 가장 대표적인 예시가 그 유명한 AlphaGo의 바둑이다. 바둑의 경우의 수는 계산 불가능의 영역이다. 그럼에도 AlphaGo가 성공했던 이유는 RL의 기반인 Bellman optimality equation을 근사적으로 잘 풀어냈기 때문이다.
References
[1] Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction; 2nd Edition. 2018.
[2] Towards Data Science. blackburn. Reinforcement Learning: Bellman Equation and Optimality (Part 2).
[3] Wikipedia. Markov decision process.