이 포스트에서는 Reinforcement learning (RL)의 기본 내용인 Multi-armed Bandits 환경과 기본적인 아이디어들에 대해 알아본다.
Reinforcement learning vs others
Reinforcement learning (RL)과 다른 learning의 가장 큰 구별점은 사용하는 정보의 차이에 있다. 다른 learning은 주로 올바른 action을 나타내는 일종의 정답 label이 존재하는 instructive feedback을 사용하며, 이러한 feedback을 사용하는 learning을 supervised learning이라고 한다. 그러나 RL에서는 evaluative feedback을 사용한다. evaluative feedback은 이것이 얼마나 좋은 action인지를 나타내지만 best action인지 아닌지를 나타내지는 않는다. 이를 unsupervised learning이라고 한다.
What is Multi-armed Bandits
Multi-armed Bandits 환경은 슬롯 머신에서 여러 개의 레버를 당겨 보상을 획득하는 환경이다. 이 때 레버의 개수를 $k$개라고 할 때 $k$-armed bandit problem이라고 하며 아래와 같은 환경으로 정의된다.
- $k$개의 다른 action들을 반복적으로 선택함.
- 각 선택에 대해 stationary probability distribution을 따르는 수치적인 reward를 획득함.
- 일정 기간(time steps) 동안의 expected total reward를 maximized하는게 목적임.
stationary probability distribution은 시간이 흐름에도 변하지 않는 정적인 확률 분포를 의미한다.
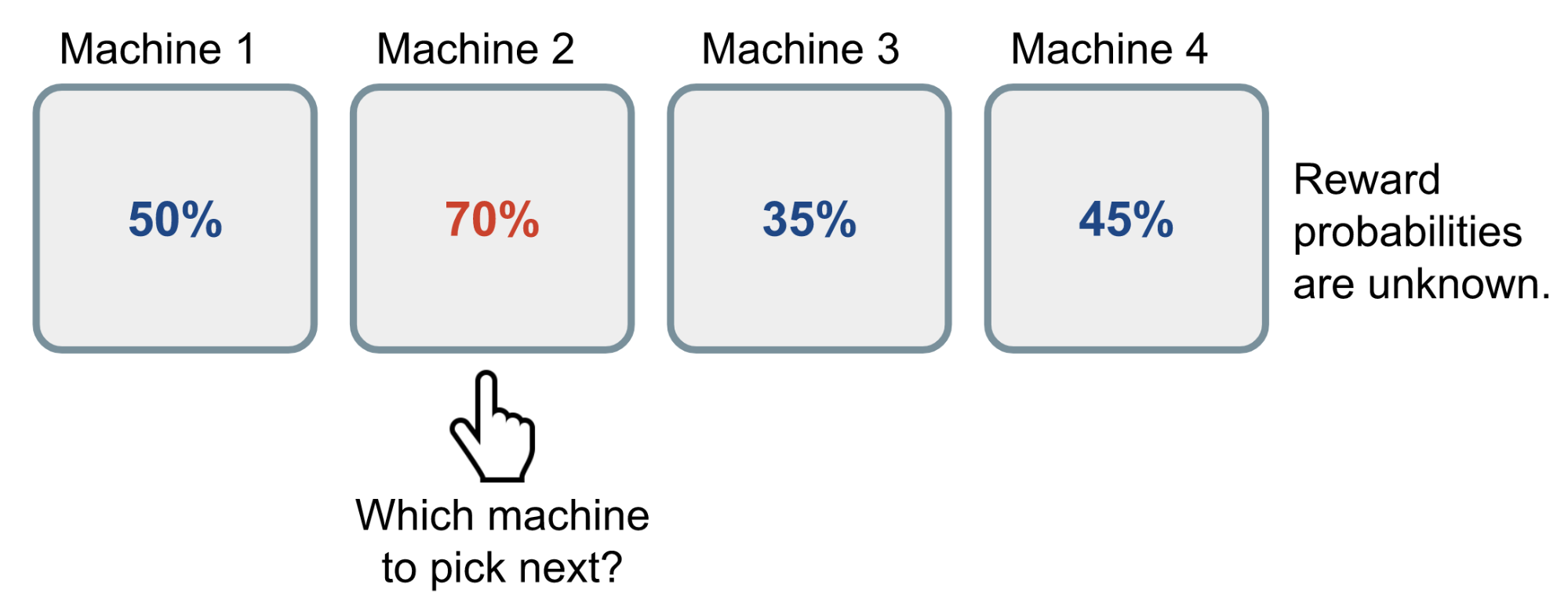Fig 1. Multi-armed bandits.
(Image source: Lil’Log.)
$k$-armed bandit problem과 일반적인 reinforcement learning problem의 가장 큰 차이점은 $k$-armed bandit problem은 어떤 상태에서 선택한 행동으로 즉각적인 보상만 획득할 뿐, 레버를 당기는 action들이 environment의 states와 future rewards를 변경시키지 않는다. 즉, actions와 states가 연관성이 없으며 이를 nonassociative setting이라고 한다. 반대로 associative setting에서는 선택한 action들이 states를 변경시켜 future rewards에 영향을 미치는 파급효과를 가진다.
$k$-armed bandit problem에서 각 time step $t$에서 선택한 action을 $A_t$, 획득한 reward을 $R_t$라고 할 때 임의의 action $a$에 대한 value $q_\ast(a)$는 $a$에 대한 expected reward이다.
\[q_\ast(a) \doteq \mathbb{E}[R_t \vert A_t = a]\]그러나 실제 $q_\ast(a)$를 모르기 때문에 우리는 이 값을 추정해야한다. time step $t$에서 추정된 action $a$의 value를 $Q_t(a)$라고 할 때 우리의 목적은 이 값을 $q_\ast(a)$에 근접시키는 것이다.
Exploitation vs Exploration
action value를 추정하는 과정에서 가장 value가 높은 action을 greedy action이라고 하며 이들에 대한 선택을 exploiting이라고 한다. 그 외의 action을 선택할 때는 exploration이라고 부른다. exploitation은 현재 가진 정보를 기준으로 즉각적인 최고의 보상을 획득할 수 있는 수단이다. 그러나 exploration은 단기간 적은 보상을 획득하지만 내가 모르는 정보를 탐색해 현재 greedy action보다 더 나은 action을 발견하여 더 높은 total reward를 획득할 수 있는 수단이다. 결국 exploitation과 exploration 사이에 적절한 선택이 필요하며 이는 그 유명한 exploitation vs exploration dilemma로 강화학습의 숙명과도 같은 문제이다.
Action-value Methods
action value를 추정하는 가장 간단한 방법은 지금까지 획득한 reward의 평균을 구하는 것이다.
\[Q_t(a) \doteq \dfrac{\sum_{i=1}^{t-1}R_i \cdot 𝟙_{A_i=a}}{\sum_{i=1}^{t-1}𝟙_{A_i=a}}\]$𝟙_{predicate}$은 $predicate$이 true이면 1, false이면 0을 반환하는 함수이다.
action value에 따라 action을 선택하는 가장 간단한 방법은 가장 높게 추정된 action value를 가진 action을 선택하는 것이다. 즉, greedy action을 선택한다.
\[A_t \doteq \underset{a}{\arg\max}\ Q_t(a)\]위 방법은 항상 exploitation을 수행하기 때문에 지금보다 더 나은 행동을 발견할 수 없다. 이에 대안 대안으로 대부분은 exploitation을 수행하되 $\epsilon$의 확률로 랜덤하게 action을 선택한다. 이를 $\epsilon$-greedy 방법이라 한다.
Incremental Implementation
어떤 단일 action의 $i$번째 선택 시 획득 한 reward를 $R_i$라고 할 때, 이 action을 $n - 1$번 선택했을 때의 action value의 추정치 $Q_n$을 $n - 1$번 획득한 reward들의 평균으로 추정한다면 아래와 같은 수식으로 표현할 수 있다.
\[Q_n \doteq \dfrac{R_1 + R_2 + \cdots + R_{n-1}}{n - 1}\]그러나 위와 같은 수식에서는 그동안 획득한 모든 reward들을 모두 기록해야하며, 새로운 reward를 획득할 때 마다 처음부터 다시 reward들을 모두 더하는 계산을 해야한다는 문제가 있다. 이에 대한 대안으로 평균을 구하는 수식을 incremental한 형태로 변경할 수 있는데 이 경우 위 수식처럼 reward들을 기록할 필요가 없으며 계산 모든 reward들을 합할 필요가 없어진다. 기존 평균 값에 새롭게 획득한 reward의 일정 비중만을 누적하면 되는 원리이다. 기존 action value $Q_n$과 새롭게 획득한 $n$번째 reward $R_n$이 있을 때 action value에 대한 incremental formula는 아래와 같다.
\[Q_{n+1} = Q_n + \dfrac{1}{n}[R_n - Q_n]\]위 수식에 대한 일반적인 형태는 아래와 같다.
\[\textit{NewEstimate} \leftarrow \textit{OldEstimate} + \textit{StepSize} \Big[\textit{Target} - \textit{OldEstimate} \Big]\]위 수식에서 $\Big[\textit{Target} - \textit{OldEstimate} \Big]$는 추정치에 대한 error이며 이를 바탕으로 점점 Target에 다가간다.
Nonstationary Problem
reward에 대한 확률들이 시간이 지나도 변하지 않는 stationary problem에서는 평균을 구하는 위 방법이 유용할 지 모르지만 nonstationary 환경에서는 그렇지 않다. 이 경우엔 지난 과거의 보상보다 최근 보상에 더 큰 비중을 주는게 합당하다. 이에 대한 하나의 방법으로 step-size를 상수로 사용한다. 아래는 이에 대한 incremental update 수식이다.
\[Q_{n+1} \doteq Q_n + \alpha[R_n - Q_n]\]step-size parameter인 $\alpha \in (0,1]$는 상수이다. 다만 $\alpha$ 값을 step에 따라 변경하는게 더 효과적일 때도 있다.
Initial Value
위 수식은 past rewards와 initial estimate $Q_1$의 weighted average로 표현될 수 있다.
\[\begin{aligned} Q_{n+1} &= Q_n + \alpha[R_n - Q_n] \\ &= (1-\alpha)^nQ_1 + \sum_{i=1}^n\alpha(1-\alpha)^{n-i}R_i \end{aligned}\]위 수식을 보면 알겠지만 현재 action value는 initial value인 $Q_1(a)$에 영향을 받는다. 즉 bias가 발생하였다. 몰론 표본평균방법일 경우 모든 action들이 적어도 한번 선택된다면 이러한 bias는 사라지지만 위 수식처럼 step-size $\alpha$가 상수일 경우 bias는 영구적이다. 그러나 $\alpha \in (0, 1]$이기 때문에 시간이 지날 수록 결국 이러한 bias는 작아지게 된다. 그렇기 때문에 이러한 bias는 실제로 그다지 문제가 되지 않는다.
Upper-Confidence-Bound Action Selection
$\epsilon$-greedy 방법은 exploration을 무차별적으로 수행하게 만든다는 문제가 있다. action value의 추정치가 최대값에 얼마나 가까운지와 불확실성은 얼마나 되는지를 모두 고려해, 실제로 최적이 될 가능성에 따라 non-greedy action들 사이에서 선택하는 것이 조금 더 효과적일 것이다. 이에 대한 대안으로 upper confidence bound (UCB) 방법이 있으며 그 수식은 아래와 같다.
\[A_t \doteq \underset{a}{\arg\max}\ \Bigg[Q_t(a) + c \sqrt{\dfrac{\ln t}{N_t(a)}} \ \Bigg]\]$N_t(a)$는 time step $t$ 이전에 action $a$가 선택된 횟수이며, $c > 0$는 exploration을 컨트롤 하는 정도로 신뢰도를 결정한다. square-root 부분은 $a$의 값에 대한 추정에서 불확실성을 나타낸다. 이를 통해 action $a$의 true value에 대한 일종의 upper bound를 설정할 수 있다. action $a$가 선택될 때에는 분자 $\ln t$가 증가하긴 하지만 분모 $N_t(a)$가 증가하기 때문에 불확실성은 대게 감소한다. 그 이유는 분자는 log-scale이지만 분모는 linear-scale이기 때문이다. $a$ 외의 다른 action이 선택될 때는 분자 $\ln t$는 증가하지만 분모 $N_t(a)$는 변하지 않기 때문에 불확실성은 증가한다. 위 수식에 따라 action value의 추정치 $Q_t(a)$가 너무 낮거나, action $a$가 너무 자주 선택됬을 경우 점점 선택되는 빈도가 줄게 된다. 어떤 action $a$의 action value $Q_t(a)$가 높아 이 action이 한동안 계속 자주 선택될 경우 이 action에 대한 불확실성은 줄어든다. 반대로 다른 action들은 그동안 선택되지 않았기 때문에 불확실성이 늘어나며 어느 순간 cross가 발생해 다른 action의 upper bound가 더 커져 다른 action을 수행하게 된다. 그러나 $t \rightarrow \infty$일 경우 분자는 log-scale이지만 분모는 linear-scale이기 때문에 결국 0으로 수렴한다. 즉, time step $t$가 작을 때는 exploration이 활발히 일어나지만 time step $t$가 증가할 수록 전체 action에 대한 불확실성은 낮아지고 결국 action value $Q_t(a)$에 대해서만 action을 선택하는 exploitation을 수행할 것이다.
UCB 방법은 $k$-armed bandits에서 $\epsilon$-greedy 보다 좋은 성능을 낸다. 그러나 좀 더 일반적인 RL setting으로 확장하는 것은 상당히 어려우며 실용적이지 못하다. UCB는 nonstationary 문제를 다루는데 어려움이 있으며 large state space에서 function approximation을 사용할 때 어려움이 있다.
Gradient Bandit Algorithms
각 action $a$에 대한 numerical preference를 $H_t(a)$를 학습하는 것을 고려해보자. preference가 클 수록 더 자주 action이 선택된다. 여기서 preference는 action value $Q_t(a)$와는 다르게 reward 측면에서 해석되지 않는다. 또한 action을 선택할 때 한 action의 preference와 다른 action들의 preference 사이의 상대적 비교로 결정한다. $k$개의 action이 있다고 할 때 각 action을 선택하는 확률은 soft-max distribution을 따르며 그 수식은 아래와 같다.
\[\text{Pr}\lbrace A_t = a \rbrace \doteq \dfrac{e^{H_t(a)}}{\sum_{b=1}^k e^{H_t(b)}} \doteq \pi_t(a)\]$\pi_t(a)$는 time step $t$에서 action을 선택하는 확률이다. preference $H_t(a)$를 학습하기 위한 방법 중 하나로 stochastic gradient ascent가 있다. action $A_t$를 선택한 뒤 reward $R_t$를 획득했을 때 action preference들은 아래와 같은 수식으로 업데이트된다.
\[H_{t+1}(a) \doteq H_t(a) + \alpha \dfrac{\partial \mathbb{E}[R_t]}{\partial H_t(a)}\]위 수식은 gradient ascent에 대한 기본적인 아이디어이며 이를 바탕으로 아래와 같은 수식을 얻을 수 있다.
\[\begin{aligned} &H_{t+1}(A_t) \doteq H_t(A_t) + \alpha(R_t - \bar{R_t})(1 - \pi_t(A_t)) & \text{and} & \\ &H_{t+1}(a) \doteq H_t(a) - \alpha(R_t - \bar{R_t})\pi_t(a) & \text{for all} \; a \neq A_t \end{aligned}\]$\bar{R_t}$는 time step $t$까지의 모든 reward의 평균이다. $\bar{R_t}$는 reward에 대한 baseline으로 획득한 reward $R_t$가 baseline보다 클 경우 $A_t$를 미래에 수행할 확률은 증가하고, baseline보다 작을 경우엔 감소한다. 선택되지 않은 나머지 action들은 $A_t$와 반대로 업데이트된다.
References
[1] Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction; 2nd Edition. 2018.
[2] Lil’Log. The Multi-Armed Bandit Problem and Its Solutions.