이 포스트에서는 reinforcement learning을 수행하는 새로운 방법인 function approximation에 대한 소개와 이를 바탕으로 on-policy method에서 prediction을 수행하는 방법을 소개한다.
What is Function Approximation and Why needed?
지금까지 알아본 기존 Reinforcement Learning (RL) 방법들은 모두 tabular 기반이었다. tabular 기반 방법들은 작은 state space에서는 잘 작동하지만 매우 큰 state space에 적용할 때는 치명적인 몇가지 문제가 발생한다.
먼저, state space가 매우 클 경우 각 state를 모두 mapping하는 데 너무 많은 메모리가 요구된다. 대부분의 RL task들은 가능한 state의 경우의 수가 우주에 존재하는 모든 원자 개수보다 많거나 실수 전체 집합에서 정의되어 무한개이다.
두 번째는 이러한 많은 state space에 대해 완벽히 계산할 시간이 없다는 것이다. state space가 클 수록 state에 mapping되는 table은 더 커질 것이고 이에 따라 더 많은 데이터가 필요하고 계산되어야 한다. 이를 수행할만한 시간은 당연히 턱없이 부족하다. 따라서 대부분의 state는 아예 발견조차 하지 못할 때가 많다.
더 좋은 학습을 위해선 아직 발견하지 못한 state에 대해서도 적절히 처리할 수 있어야 한다. 이를 위해 state를 일반화할 필요성이 있다. 즉, 주요 이슈는 generalization이다. 일반화를 달성할 수 있는 방법으로 function approximation을 사용한다. function approximation은 말 그대로 함수를 근사하는 방법이다. function approximation은 원래 supervised learning에서 사용되던 방법이다. 이를 RL에 적용해 state에 대한 function을 (e.g., value function, policy) 근사하는 것이 앞으로의 주요 과제이다.
function approximation을 RL에 적용할 때 전통적인 supervised learning에서는 나타나지 않던 몇가지 문제가 발생한다. 대표적으로 nonstationarity, bootstrapping, delayed target이 있다. 이 문제를 포함한 function approximation을 RL에 적용할 때 발생하는 여러 문제들을 우리는 앞으로 다룰 것이다.
Introduction
이 포스트에서는 function approximation을 적용한 on-policy method에 집중할 것이다. on-policy method는 policy $\pi$로부터 생성된 experience로부터 $\pi$에 대한 함수를 추정하는 방법이었다. 여기서는 $\pi$에 대한 state-value function $v_\pi$를 근사하는 방법을 알아볼 것이다.
기존 tabular 기반 방법과의 가장 주요한 차이점은 추정된 value function이 table이 아닌 weight vector $\mathbf{w} \in \mathbb{R}^d$로 구성된 매개변수화된 함수로써 표현된다는 것이다. 따라서 어떤 weight vector $\mathbf{w}$가 주어졌을 때 state $s$에 대한 근사값을 $\hat{v}(s,\mathbf{w}) \approx v_\pi(s)$로 나타낸다. 요즘 대부분의 RL은 weight vector $\mathbf{w}$에 주로 신경망 매개변수를 사용한다. weight의 개수 ($\mathbf{w}$의 차원)는 거의 대부분의 경우 state의 개수보다 훨씬 작다. 즉, $d \ll \vert \mathcal{S} \vert$이다.
weight 하나를 변경하면 많은 state에 대한 추정치도 변하게 된다. 결과적으로 어떤 state 하나가 업데이트되면 다른 수많은 state의 value에도 영향을 미친다. 이를 통해 generalization이 가능해진다. 발견한 state에 대해 업데이트하면 아직 발견하지 못한 state의 value도 변경되기 때문이다. 그러나 다른 수많은 state의 value가 변경되기 때문에 관리하고 이해하기 어렵다는 점도 있다.
Value-function Approximation
value function을 업데이트하기 위해서는 이에 대한 target이 필요하다. target은 추정치가 다가가려는 지향점으로 생각할 수 있다. 우리는 앞선 여러 tabular 기반 방법에서 각 방법에 대한 target들을 알아봤었다. state $s$에서의 update target을 $u$라고 할 때 update를 아래와 같이 표현한다.
\[\Large s \mapsto u\]Monte Carlo (MC) update는 $S_t \mapsto G_t$, TD(0) update는 $S_t \mapsto R_{t+1} + \gamma \hat{v}(S_{t+1},\mathbf{w}_ t)$, $n$-step TD update는 $S_t \mapsto G_{t:t+n}$이다. 또한 Dynamic Programming (DP)의 policy-evaluation update는 $s \mapsto \mathbb{E}_ \pi [R_{t+1} + \gamma \hat{v}(S_{t+1},\mathbf{w}_t) \ \vert \ S_t=s]$ 이다.
이러한 update를 training example로 사용함으로써 value prediction에 대한 function approximation을 수행할 것이다. 각 update를 training example로 간주하는 것은 이미 존재하는 여러 function approximation 방법을 사용할 수 있게 해준다. 하지만 모든 function approximation이 RL에 적합하지는 않다. 대부분의 신경망 기반 방법들은 static한 여러 개의 training example로 구성된 training set을 가정한다. RL에서는 agent가 environment와 상호작용하면서 online으로 학습하는 것이 중요하다. 따라서 점진적으로 획득한 data로부터 효과적으로 학습할 수 있는 방법이 필요하다. 게다가 RL에서는 일반적으로 function approximation 방법이 nonstationary한 target function을 (시간이 지남에 따라 target function이 변함) 다룰 수 있어야 한다. 일반적인 supervised learning은 target인 정답 레이블이 고정되어 있기 때문에 이러한 문제가 발생하지 않는다.
The Prediction Objective ($\overline{\text{VE}}$)
function approximation을 사용할 경우 발생하는 문제는 어떤 state에서의 update가 다른 state에도 영향을 미친다는 것이다. state의 개수는 weight의 개수보다 훨씬 많으며 이로 인해 한 state의 추정치를 정확하게 만들면 다른 나머지는 덜 정확해진다. 따라서 모든 state에 대한 정확한 값을 얻는 것은 불가능하다.
위와 같은 이유로 우리는 어떤 state에 조금 더 집중할 지를 고민할 필요가 있다. 즉, 상대적으로 중요하다고 여겨지는 state를 더 정확히 추정한다. 어떤 state를 정확히 추정할 수록 그 state의 추정치 $\hat{v}(s,\mathbf{w})$와 실제값 $v_\pi(s)$의 오차는 작을 것이다. 상대적으로 중요하다고 여겨지는 state의 오차를 더 많이 줄이고 싶다. 이를 위해 얼마나 그 state에 집중할 지를 나타내는 state distribution을 $\mu(s) \geq 0, \sum_s \mu(s) = 1$라고 하자. $\mu$에 의해 state space에 가중치를 부여함으로써 오차에 대한 objective function을 아래와 같이 정의할 수 있다.
\[\overline{\text{VE}}(\mathbf{w}) \doteq \sum_{s \in \mathcal{S}}\mu(s)\Big[v_\pi(s) - \hat{v}(s,\mathbf{w}) \Big]^2\]위 objective function을 mean square value error라고 한다. 그러나 RL에서 $\overline{\text{VE}}$를 minimize한다고 해서 좋은 성능을 낸다고 말할 수는 없다. RL의 궁극적인 목적은 더 좋은 policy를 찾는 것이고, 이를 위해 value function을 학습하는 것이다.
function approximation을 사용할 경우 $\overline{\text{VE}}$의 global optimum을 보장할 수 있을까? 간단한 linear method에 대해서는 보장되지만, 신경망과 같은 복잡한 function approximator의 경우 global optimum이 아닌 대게 weight vector $\mathbf{w}^\ast$의 근처에 있는 모든 $\mathbf{w}$에 대해서만 $\overline{\text{VE}}(\mathbf{w}^\ast) \leq \overline{\text{VE}}(\mathbf{w})$를 만족하는 local optimum에 수렴하려고 한다. 그러나 이마저도 대부분의 강화학습에서는 수렴성에 대한 보장이 없으며 오히려 $\overline{\text{VE}}$가 발산하는 경우도 생긴다.
Stochastic-gradient and Semi-gradient Methods
이번 포스트의 핵심이다. Stochastic Gradient Descent (SGD)는 function approximation을 위한 가장 대표적인 학습 방법으로 online RL에도 잘 작동한다. SGD를 사용해 value prediction을 수행해보자.
weight vector는 $d$개의 실수로 구성되어 있는 열벡터로 $\mathbf{w} \doteq (w_1,w_2,\dots,w_d)^\top$이다. approximate value function $\hat{v}(s,\mathbf{w})$는 모든 state $s \in \mathcal{S}$에서 $\mathbf{w}$에 대해 미분가능한 함수이다. time step $t$마다 $\mathbf{w}$를 업데이트하며 각 time step에서의 weight vector를 $\mathbf{w}_t$로 나타낸다.
각 time step마다 새로운 example $S_t \mapsto v_\pi(S_t)$를 관찰한다고 하자. 또한 동일한 distribution $\mu$를 가진 state가 example에 나타난다고 하자. 이 때 관찰된 example에 대해 error $\overline{\text{VE}}$를 minimize하기 위해 SGD method를 사용해 weight vector를 error를 줄이는 방향으로 조정한다. SGD는 gradient descent method로 기울기의 반대 방향으로 약간 이동해 함수를 minimize하는 최적화 방법이다. 업데이트가 확률적으로 선택된 단일 example에 대해 수행될 때 gradient descent method를 “stochastic”하다고 부른다. 아래는 이에 대한 수식이다.
\[\begin{align} \mathbf{w}_{t+1} &\doteq \mathbf{w}_t - \dfrac{1}{2}\alpha \nabla \Big[ v_\pi(S_t) - \hat{v}(S_t, \mathbf{w}_t) \Big]^2 \\ &= \mathbf{w}_t + \alpha \Big[v_\pi(S_t) - \hat{v}(S_t, \mathbf{w}_t) \Big] \nabla \hat{v}(S_t, \mathbf{w}_t) \end{align}\]$\alpha$는 양수인 step-size parameter이다. $\nabla f(\mathbf{w})$는 gradient vector로 함수 $f(\mathbf{w})$를 편미분한 열벡터이다.
\[\nabla f(\mathbf{w}) \doteq \bigg(\dfrac{\partial f(\mathbf{w})}{\partial w_1}, \dfrac{\partial f(\mathbf{w})}{\partial w_2}, \cdots , \dfrac{\partial f(\mathbf{w})}{\partial w_d} \bigg)^\top\]기울기의 반대 방향으로 약간만 이동하는 이유는 각기 다른 state들에 대한 error의 균형을 맞추는 근사를 하기 위해서이다. error를 완전히 없애는 value function을 찾는 것이 목적이 아닐 뿐더러, 모든 state에 대한 정확한 실제값을 알고 있더라도, $d \ll \vert \mathcal{S} \vert$인 weight vector $\mathbf{w}$의 제한된 차원으로 인해 error를 완전히 없애는 것은 불가능하다. 또한 SGD는 $\alpha$가 시간에 따라 감소한다고 가정하며 이 경우 local optimum으로의 수렴이 보장된다. 따라서 약간만 이동하는 것이 바람직하다.
General-gradient Method
RL은 supervised learning과 다르게 정답 레이블이 존재하지 않는 unsupervised learning이다. 따라서 target의 실제값 $v_\pi(S_t)$를 알지 못한다. t번째 training example의 실제 값이 아닌 target을 $U_t \in \mathbb{R}$라고 하자. 즉, $S_t \mapsto U_t$이다. $v_\pi(S_t)$를 $U_t$로 대체하더라도 여전히 SGD를 통해 근사화가 가능하다.
\[\mathbf{w}_{t+1} \doteq \mathbf{w}_t + \alpha \Big[U_t - \hat{v}(S_t, \mathbf{w}_t) \Big] \nabla \hat{v}(S_t, \mathbf{w}_t)\]만약 $U_t$가 unbiased 추정치라면, 즉, $\mathbb{E}[U_t \vert S_t=s] = v_\pi(s)$라면 $\mathbf{w}_ t$는 local optimum으로 수렴됨이 보장된다. 대표적으로 Monte Carlo target $U_t \doteq G_t$는 $v_\pi(S_t)$의 unbiased 추정치이기 때문에 위 조건을 만족한다. 아래 박스는 Monte Carlo 방법을 사용한 value prediction 알고리즘이다.
$\text{Algorithm: Gradient Monte Carlo Algorithm for Estimating $\hat{v} \approx v_\pi$}$
\(\begin{align*} & \textstyle \text{Input: the policy $\pi$ to be evaluated} \\ & \textstyle \text{Input: a differentiable function } \hat{v} : \mathcal{S} \times \mathbb{R}^d \rightarrow \mathbb{R} \\ & \textstyle \text{Algorithm parameter: step size } \alpha > 0 \\ & \textstyle \text{Initialize value-function weights $\mathbf{w} \in \mathbb{R}^d$ arbitrarily (e.g., $\mathbf{w}=\mathbf{0}$)} \\ \\ & \textstyle \text{Loop forever (for each episode):} \\ & \textstyle \qquad \text{Generate an episode } S_0, A_0, R_1, S_1, A_1, \dots, R_T, S_T \text{ using } \pi \\ & \textstyle \qquad \text{Loop for each step of episode, } t = 0, 1, \dots, T-1 \text{:} \\ & \textstyle \qquad\qquad \mathbf{w} \leftarrow \mathbf{w} + \alpha [G_t - \hat{v}(S_t, \mathbf{w})] \nabla \hat{v}(S_t, \mathbf{w}) \\ \end{align*}\)
Semi-gradient Method
MC method와는 다르게 TD method나 DP는 bootstrapping을 통해 target을 근사화한다. bootstrapping target은 weight vector $\mathbf{w}_ t$에 의한 현재 추정치에 의존한다. 따라서 bootstrapping target은 biased해 unbiased target과 같은 local optimum으로의 수렴이 보장되지 않는다.
bootstrapping 방법은 추정치에 대해서 weight vector $\mathbf{w}_ t$를 변경하는 것은 고려하지만, target에 대해서는 고려하지 않는다. 즉, gradient의 일부분만을 포함하기 때문에 semi-gradient method라고 부른다.
수렴성에 대한 보장이 없음에도 불구하고 bootstrapping 방법은 MC method보다 더 선호된다. MC method와 달리 episode의 종료를 기다릴 필요가 없어 continuing task에도 적용할 수 있고, online으로 학습이 가능해 훨씬 빠른 학습 속도를 가진다.
아래 박스는 가장 대표적인 semi-gradient method인 semi-gradient TD(0)의 알고리즘이다.
$\text{Algorithm: Semi-gradient TD(0) for estimating } \hat{v} \approx v_\pi$
\(\begin{align*} & \textstyle \text{Input: the policy $\pi$ to be evaluated} \\ & \textstyle \text{Input: a differntiable function $\hat{v} : \mathcal{S}^+ \times \mathbb{R}^d \rightarrow \mathbb{R}$ such that } \hat{v}(\text{terminal}, \cdot) = 0 \\ & \textstyle \text{Algorithm parameter: step size } \alpha > 0 \\ & \textstyle \text{Initialize value-function weights $\mathbf{w} \in \mathbb{R}^d$ arbitrarily (e.g., $\mathbf{w}=\mathbf{0}$)} \\ \\ & \textstyle \text{Loop for each episode:} \\ & \textstyle \qquad \text{Initialize } S \\ & \textstyle \qquad \text{Loop for each step of episode:} \\ & \textstyle \qquad\qquad \text{Choose } A \sim \pi(\cdot \vert S) \\ & \textstyle \qquad\qquad \text{Take action $A$, observe } R, S' \\ & \textstyle \qquad\qquad \mathbf{w} \leftarrow \mathbf{w} + \alpha [R + \gamma \hat{v}(S', \mathbf{w}) - \hat{v}(S, \mathbf{w})] \nabla \hat{v}(S,\mathbf{w}) \\ & \textstyle \qquad\qquad S \leftarrow S' \\ & \textstyle \qquad \text{until $S$ is terminal} \\ \end{align*}\)
위 알고리즘을 보면 왜 semi-gradient method인지 알 수 있다. TD(0)의 target은 $U_t \doteq R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w_t})$이다. weight vector $\mathbf{w}_ t$에 의한 next state의 value 추정치를 사용해 target이 구성되고 error를 구하지만, gradient vector는 target이 아닌 현재 state의 추정치만을 고려하고 있음을 알 수 있다.
Nonlinear Function Approximation: Artificial Neural Networks
Artificial Neural Network (ANN)은 nonlinear function approximation에 널리 사용되는 방법이다. ANN은 뉴런이 서로 연결되어있는 네트워크이다. 아래 그림은 일반적인 feedforward ANN을 나타낸다. 4개의 입력 유닛으로 구성된 input layer와 2개의 출력 유닛으로 구성된 output layer, 2개의 “hidden layer”로 구성되어있다.
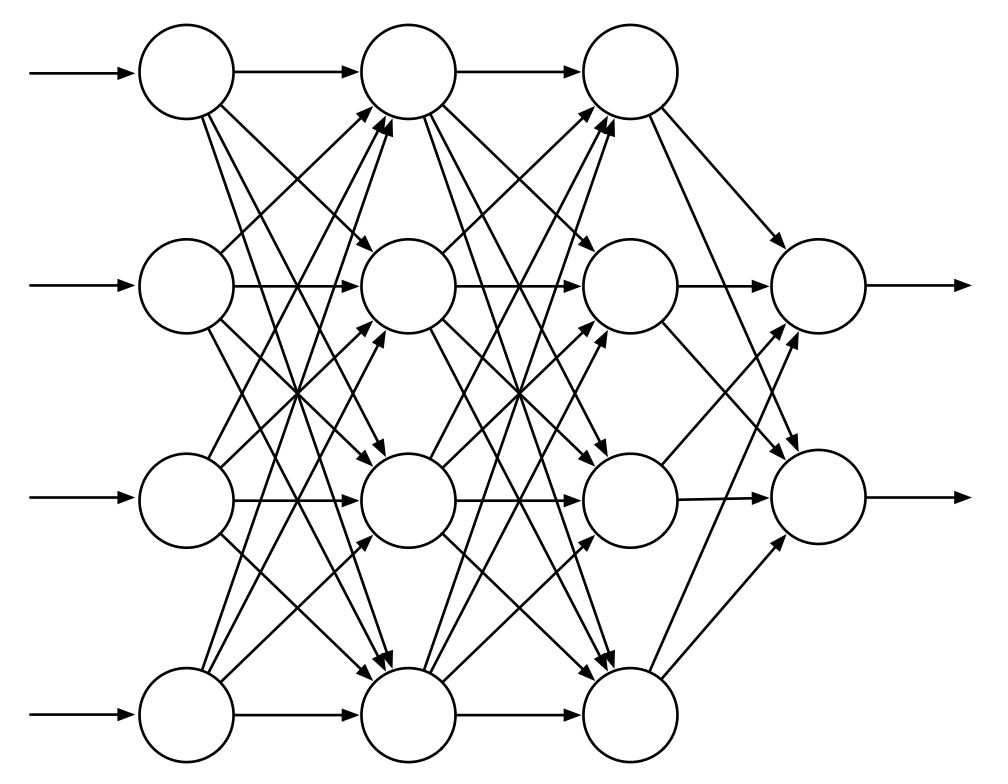Fig 1. A generic feedforward ANN with 4 input units, 2 output units, and 2 hidden layers.
(Image source: Sec 9.7 Sutton & Barto (2020).)
각각의 weight는 각 링크(그림에서 화살표)에 대응된다. 각 유닛은 semi-linear 유닛으로 입력 신호의 weighted sum을 구하는 linear 연산 후, nonlinear function인 activation function에 적용하여 유닛의 출력인 activation을 얻는다. 중요한 점은 activation function은 반드시 nonlinear function이어야 한다.
feedforward ANN의 각 출력 유닛의 activation은 nonlinear function이다. 이 함수는 network의 연결 weight에 의해 매개변수화된다. hidden layer가 없는 ANN은 가능한 함수의 굉장히 작은 부분만 표현할 수 있다. 그러나 충분히 큰 개수의 유닛을 가진 hidden layer가 있을 경우 network의 input space에 대해 좁은 영역에서 어떤 연속 함수든지 근사화할 수 있다.
ANN은 일반적으로 stochastic gradient method에 의해 학습되며, 각 weight는 minimize하거나 maximize할 objective function에 의해 측정된 네트워크의 전체적인 성능을 향상시키는 방향으로 조정된다. 일반적인 supervised learning의 경우 objective function은 training example에 대한 expected error이다. 반면 RL에서는 value function을 학습하기 위한 TD error, maximizing expected reward, policy-gradient algorithm 등 여러 종류의 objective function을 사용한다.
복잡한 구조의 ANN을 효과적으로 미분하는 방법은 그 유명한 backpropagation algorithm이다. backpropagation algorithm은 1개나 2개의 hidden layer로 구성된 얕은 network에 대해서는 상당히 좋은 결과를 낸다. 그러나 보다 더 깊은 deep ANN에서는 한계가 있다. 그 이유는 먼저, 굉장히 많은 weight로 구성된 deep ANN은 overfitting 문제를 피하기 어렵다는 점이다. overfitting은 아직 훈련하지 않은 case에 대해 일반화하는 데 실패하는 문제이다. 두번째는, backpropagation을 통해 계산된 편미분 값이 입력층에 도달할 수록 가파르게 감소해 학습이 극도로 느려지거나, 가파르게 증가해 학습을 불안정하게 만들기 때문이다. 그러나 최근에는 이 문제를 다루는 여러 방법들이 많이 나와 hidden layer가 굉장히 많은 매우 깊은 network도 잘 학습한다.
References
[1] Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction; 2nd Edition. 2020.