Policy Gradient Methods

드디어 긴 장정 끝에 대망의 마지막 챕터로 왔다. 이번 포스트에서는 그 유명한 policy gradient method에 대해 소개하려고 한다. 길고 긴 여정이 드디어 끝났다.

Introduction

지금까지 우리는 value-based 기반의 방법을 다뤘었다. policy는 추정된 action value에 기반해 action을 선택했다. 이번에는 policy 자체를 매개변수화된 함수로써 학습하는 방법을 볼 것이다. policy parameter vector를 $\mathbf{\theta} \in \mathbb{R}^{d’}$라고 할 때 policy를 parameter $\mathbf{\theta}$가 주어졌을 때 action $a$를 선택하는 확률로써 정의할 수 있다.

\[\pi(a \vert s, \mathbf{\theta}) = \Pr\{A_t = a \ \vert \ S_t = s, \mathbf{\theta}_t = \mathbf{\theta} \}\]

policy parameter에 관한 scalar 성능 수치 $J(\mathbf{\theta})$가 있다고 하자. policy를 이 수치에 대한 gradient에 기반해 policy parameter를 학습할 것이다. 이 성능 수치를 maximize하는 것이 목적이며 이에 따라 $J$에 대해 gradient ascent를 수행한다.

\[\mathbf{\theta}_{t+1} + \mathbf{\theta}_t + \alpha \widehat{\nabla J(\mathbf{\theta}_t)}\]

$\widehat{\nabla J(\mathbf{\theta}_t)} \in \mathbb{R}^{d’}$는 stochastic 추정치로, 이것의 기대값은 성능 수치의 gradient를 근사화한다. 이러한 일반적인 schema를 따르는 모든 방법들을 policy gradient methods라고 부른다.

Policy Approximation and its Advantages

policy gradient method에서는 $\pi(a \vert s, \mathbf{\theta})$가 미분 가능하다. 또한 exploration을 보장하기 위해 일반적으로 policy는 절대 deterministic하지 않으며 즉, stochastic (i.e., $\pi(a \vert s, \mathbf{\theta}) \in (0, 1), \text{ for all } s, a, \mathbf{\theta}$) 하다. policy-based method는 discrete action space 뿐만 아니라 continuous action space에서도 쉽게 적용 가능하다는 엄청난 장점이 있다.

action space가 discrete이고 너무 크지 않다고 하자. 이때 state-action pair에 대한 매개변수화된 수치적인 선호도를 $h(s, a, \mathbf{\theta})$라고 한다면, 아래와 같이 policy $\pi$를 soft-max distribution으로 정의할 수 있다.

\[\pi(a \vert s, \mathbf{\theta}) \doteq \dfrac{e^{h(s,a,\mathbf{\theta})}}{\sum_b e^{h(s,b,\mathbf{\theta})}}\]

이러한 방식이 가지는 이점은 크게 아래와 같다.

1. policy가 점점 deterministic policy로 다가가도록 근사화됨
2. 임의의 확률을 가진 action 선택을 가능하게 함
3. policy가 종종 근사화하기에 더 단순한 함수이며 학습 속도가 빠름
4. 사전 지식을 주입하기에 더 좋음

1번의 경우 어떤 state에서의 optimal policy가 deterministic할 때 policy-based method는 deterministic 하도록 근사화하지만, action-value method는 $\epsilon$-greedy policy를 사용할 때 항상 $\epsilon$의 확률로 랜덤하게 action을 선택해야 한다.

$\epsilon$을 0으로 설정하면 다른 state에서도 deterministic하게 되므로 결코 바람직 하지 않음

2번의 경우 카드게임 같은 확률 게임을 생각해볼 수 있다. 이러한 게임들은 optimal policy가 stochastic하다. 아래 그림을 보면 왜 $\epsilon$-greedy에 비해 훨씬 우월한지 알 수 있다.

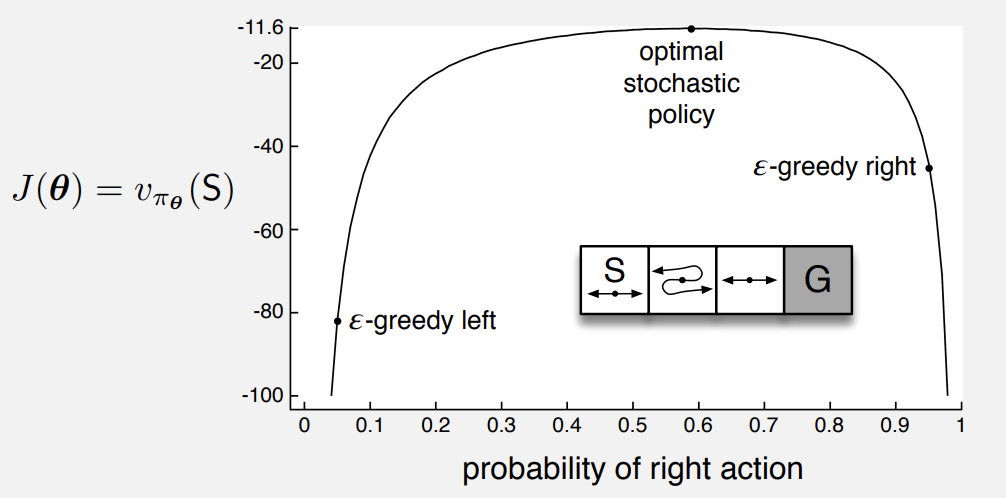Fig 1. When optimal policy is stochastic.
(Image source: Sec 13.1 Sutton & Barto (2020).)

위 그림은 $\epsilon = 0.1$일 때의 상황으로 optimal (약 0.59의 확률)에 비해 획득한 value가 훨씬 낮다.

The Policy Gradient Theorem

policy 매개변수화에 대한 중요한 이론적인 이점이 하나 더 있다. 연속적인 policy 매개변수화는 action 선택 확률을 학습된 parameter의 함수로써 부드럽게 변화시킨다. 반면 $\epsilon$-greedy는 매우 작은 변화로 maximum action value를 가지는 action이 변경되면 확률이 급격히 변경된다. 따라서 policy-gradient method는 수렴성이 더 강력히 보장된다.

성능 수치 $J(\mathbf{\theta})$는 episodic과 continuing task에서 다르게 정의되긴 한다. 이 포스트에서는 episodic case에 대해서만 다룬다. 성능 수치를 episode의 시작 state에서의 value로 정의하자. 모든 episode는 특정한 state $s_0$에서 시작한다고 할 때 아래와 같이 정의된다.

\[J(\mathbf{\theta}) \doteq v_{\pi_\mathbf{\theta}}(s_0)\]

$v_{\pi_\mathbf{\theta}}$는 $\pi_\mathbf{\theta}$에 대한 true value function이다. 여기서는 no discounting ($\gamma = 1$)을 가정한다.

성능 개선을 보장하는 방향으로 policy parameter를 변경해야 한다. 문제는 성능이 action 선택과 state distribution에 의존한다는 점이다. action 선택은 별 문제되지 않지만 state distribution은 다르다. 우리는 일반적으로 state distribution을 모른다. 이것은 environment의 함수이기 때문이다.

policy gradient theorem을 통해 이 문제를 쉽게 해결할 수 있다. state distribution에 대한 미분을 포함하지 않고, policy parameter에 관한 성능의 gradient에 대한 analytic 표현을 제공한다. 아래는 episodic case에 대한 policy gradient theorem이다.

\[\nabla J(\mathbf{\theta}) \propto \sum_s \mu(s) \sum_a q_\pi(s, a) \nabla \pi(a \vert s, \mathbf{\theta})\]

$\propto$는 “비례한다”의 의미이다. distribution $\mu$는 $\pi$하에서의 on-policy distribution이다.¹

이제 policy gradient theorem 증명 과정을 살펴보자. notation의 단순화를 위해 $\pi$는 $\mathbf{\theta}$의 함수이며, 모든 gradient는 $\mathbf{\theta}$에 관한 것임을 암시적으로 나타낸다. 먼저 시작은 state-value function의 gradient를 action-value function에 관해 나타내는 것으로 시작한다.

\[\begin{align} \nabla v_\pi(s) &= \nabla \bigg[ \sum_a \pi(a \vert s) q_\pi(s,a) \bigg], \quad \text{for all $s \in \mathcal{S}$} \\ &= \sum_a \Big[ \nabla \pi(a \vert s) q_\pi(s,a) + \pi(a \vert s) \nabla q_\pi(s,a) \Big] \quad \text{(product rule of calculus)} \\ &= \sum_a \Big[ \nabla \pi(a \vert s) q_\pi(s,a) + \pi(a \vert s) \nabla \sum_{s',r}p(s',r \vert s,a)\big(r + v_\pi(s')\big) \Big] \quad (\because q_\pi(s, a) \doteq \sum_{s', r} p(s', r \vert s, a) \Big[r + \gamma v_\pi(s') \Big]) \\ &= \sum_a \Big[ \nabla \pi(a \vert s) q_\pi(s,a) + \pi(a \vert s) \sum_{s'}p(s' \vert s,a) \nabla v_\pi(s') \Big] \quad (\because p(s' \vert s, a) \doteq \sum_{r \in \mathcal{R}}p(s', r \vert s, a)) \\ &= \sum_a \Big[ \nabla \pi(a \vert s) q_\pi(s,a) + \pi(a \vert s) \sum_{s'}p(s' \vert s,a) \quad \text{(unrolling)} \\ &\quad\quad \sum_{a'} \big[\nabla \pi(a' \vert s') q_\pi(s',a') + \pi(a' \vert s')\sum_{s''}p(s'' \vert s',a') \nabla v_\pi(s'') \big] \Big] \\ &= \sum_{x \in \mathcal{S}} \sum_{k=0}^\infty \Pr(s \rightarrow x, k, \pi) \sum_a \nabla \pi(a \vert x) q_\pi(x,a) \end{align}\]

$p(s’ \vert s, a)$²와 $q_\pi(s, a)$³의 변환 원리는 MDP에 관한 포스트를 참고하기 바란다. unrolling을 반복한 이후의 $\Pr(s \rightarrow x, k, \pi)$는 policy $\pi$를 따를 때 $k$ time step에서의 state $s$에서 $x$로 transition이 발생할 확률이다.

앞서 우리의 목적함수 $J(\mathbf{\theta}) = v_\pi(s_0)$였다. 위에서 구한 $\nabla v_\pi(s)$를 통해 $\nabla v_\pi(s_0)$를 구해보자.

\[\begin{align} \nabla J(\mathbf{\theta}) &= \nabla v_\pi(s_0) \\ &= \sum_s \Bigg( \sum_{k=0}^\infty \Pr(s_0 \rightarrow s, k, \pi) \Bigg) \sum_a \nabla \pi(a \vert s) q_\pi(s,a) \\ &= \sum_s \eta(s) \sum_a \nabla \pi(a \vert s) q_\pi(s,a) \quad (\text{$\eta(s)$ is the expected number of visits}) \\ &= \sum_{s'} \eta(s') \sum_s \dfrac{\eta(s)}{\sum_{s'}\eta(s')} \sum_a \nabla \pi(a \vert s) q_\pi(s,a) \\ &= \sum_{s'} \eta(s') \sum_s \mu(s) \sum_a \nabla \pi(a \vert s) q_\pi(s, a) \\ &\propto \sum_s \mu(s) \sum_a \nabla \pi(a \vert s) q_\pi(s, a) \quad (\text{Q.E.D.}) \end{align}\]

드디어 모든 증명이 끝났다. 기대 방문 횟수 $\eta$와 state distribution $\mu$의 관계는 sutton 책에 자세히 기술되어 있으니 참고하기 바란다.⁴

REINFORCE: Monte Carlo Policy Gradient

자, 이제 본격적으로 실제 사용되는 policy gradient method를 알아보려고 한다. policy gradient theorem의 우측항은 target policy $\pi$를 따를 때 얼마나 자주 state들이 나타나는지에 의한 weighted sum이다. 따라서 이를 실제 state $S_t$에서의 $\pi$에 관한 기대값으로 표현할 수 있다.

\[\begin{align} \nabla J(\mathbf{\theta}) &\propto \sum_s \mu(s) \sum_a q_\pi(s,a) \nabla \pi(a \vert s, \mathbf{\theta}) \\ &= \mathbb{E}_\pi\Bigg[\sum_a q_\pi(S_t,a) \nabla \pi(a \vert S_t, \mathbf{\theta}) \Bigg] \end{align}\]

이를 통해 stochastic gradient-ascent를 수행할 수 있다.

\[\mathbf{\theta}_{t+1} \doteq \mathbf{\theta}_t + \alpha \sum_a \hat{q}(S_t, a, \mathbf{w}) \nabla \pi(a \vert S_t, \mathbf{\theta})\]

$\hat{q}$은 $q_\pi$의 학습된 근사치이다. 위 방법은 모든 action을 포함하기 때문에 all-actions method라고 부른다.

그러나 우리는 모든 action을 고려하기 보다는, 실제 선택된 action에 대해 고려하고 싶다. 이를 수행하는 가장 간단하면서도 유명한 REINFORCE 알고리즘이 있다. 아래는 위 수식으로부터 REINFORCE 알고리즘을 유도하는 과정이다.

\[\begin{align} \nabla J(\mathbf{\theta}) &\propto \mathbb{E}_\pi \Bigg[ \sum_a \pi(a \vert S_t, \mathbf{\theta}) q_\pi(S_t, a) \dfrac{\nabla \pi(a \vert S_t, \mathbf{\theta})}{\pi(a \vert S_t, \mathbf{\theta})} \Bigg] \\ &= \mathbb{E}_\pi \Big[ q_\pi(S_t, A_t) \dfrac{\nabla \pi(A_t \vert S_t, \mathbf{\theta})}{\pi(A_t \vert S_t, \mathbf{\theta})} \Big] \quad \text{(replacing $a$ by the sample $A_t \sim \pi$)} \\ &= \mathbb{E}_\pi \Big[G_t \dfrac{\nabla \pi(A_t \vert S_t, \mathbf{\theta})}{\pi(A_t \vert S_t, \mathbf{\theta})}] \quad \text{(because $\mathbb{E}_\pi[G_t \vert S_t, A_t] = q_\pi(S_t, A_t)$)} \\ &= \mathbb{E}_\pi \Big[G_t \nabla \ln \pi(A_t \vert S_t, \mathbf{\theta}) \Big] \quad \text{(logarithmic derivative)} \end{align}\]

위 과정을 차례차례 보자. action $a$에 대한 합을, policy $\pi$를 따를 때의 기대값에 의해 실제 선택된 action $A_t$로 대체하고 싶다. 그러기 위해서는 action $a$를 policy $\pi(a \vert S_t, \mathbf{\theta})$에 의해 가중치를 부여하면 된다. 이렇게 되면 policy $\pi$를 따를 때 실제 선택된 action에 대한 기대값과 동일하다. 수식의 동등성을 유지하기 위해 $\pi(a \vert S_t, \mathbf{\theta})$를 곱하고 나눈다.

마지막 라인이 우리가 얻고 싶었던 수식이다. $G_t$는 일반적인 return이며, $G_t \nabla \ln \pi(A_t \vert S_t, \mathbf{\theta})$는 각 time step에서 sampling된 값으로, 이것의 기대값은 gradient에 비례한다. 이를 통해 stochastic gradient ascent 알고리즘, REINFORCE 업데이트를 수행한다.

\[\mathbf{\theta}_{t+1} \doteq \mathbf{\theta}_t + \alpha G_t \nabla \ln \pi(A_t \vert S_t, \mathbf{\theta}_t)\]

REINFORCE는 time step $t$에서의 실제 return을 사용한다. 따라서 REINFORCE는 Monte Carlo (MC) method로, episode가 종료되어야만 모든 업데이트가 수행된다. 아래는 REINFORCE 알고리즘이다.

$\text{Algorithm: REINFORCE: Monte-Carlo Policy-Gradient Control (episodic) for $\pi_\ast$}$

\(\begin{align*} & \textstyle \text{Input: a differentiable policy parameterization $\pi(a \vert s, \mathbf{\theta})$} \\ & \textstyle \text{Algorithm parameter: step size $\alpha > 0$} \\ & \textstyle \text{Initialize policy parameter $\mathbf{\theta} \in \mathbb{R}^{d'}$ (e.g., to $\mathbf{0}$)} \\ \\ & \textstyle \text{Loop forever (for each episode):} \\ & \textstyle \qquad \text{Generate an episode $S_0, A_0, R_1, \dots, S_{T-1}, A_{T-1}, R_T$, following $\pi(\cdot \vert \cdot, \mathbf{\theta})$} \\ & \textstyle \qquad \text{Loop for each step of the episode $t = 0, 1, \dots, T - 1$:} \\ & \textstyle \qquad\qquad G \leftarrow \sum_{k = t+1}^T \gamma^{k-t-1}R_k \\ & \textstyle \qquad\qquad \mathbf{\theta} \leftarrow \mathbf{\theta} + \alpha \gamma^t G \nabla \ln \pi(A_t \vert S_t, \mathbf{\theta}) \\ \end{align*}\)

한 가지 차이점은, REINFORCE 업데이트 시의 discount factor $\gamma^t$이다. 앞서 policy gradient theorem에서 non-discounted case ($\gamma=1$)을 가정했었지만, 여기서는 일반적인 discounted setting이기 때문에 추가되었다.

REINFORCE는 $\alpha$가 시간에 따라 감소한다고 할 때 local optimum으로의 수렴성이 보장된다. 그러나 MC method 특성 상 분산이 크고, 학습 속도가 느리다.

REINFORCE with Baseline

policy gradient theorem은 임의의 action value와 baseline $b(s)$의 비교를 포함하도록 일반화 될 수 있다.

\[\nabla J(\mathbf{\theta}) \propto \sum_s \mu(s) \sum_a \Big(q_\pi(s,a) - b(s) \Big) \nabla \pi(a \vert, \mathbf{\theta})\]

baseline은 어떤 것도 가능하며, 심지어 난수도 가능하다. 위 수식이 성립하는 이유는 baseline에 의해 빼는 값이 0이기 때문이다.

\[\sum_a b(s) \nabla \pi(a \vert s, \mathbf{\theta}) = b(s) \nabla \sum_a \pi(a \vert s, \mathbf{\theta}) = b(s) \nabla 1 = 0\]

위에 따라 REINFORCE에도 baseline을 적용하는 것이 가능하다.

\[\mathbf{\theta}_{t+1} \doteq \mathbf{\theta}_t + \alpha \Big(G_t - b(S_t) \Big) \nabla \ln \pi(A_t \vert S_t, \mathbf{\theta}_t)\]

baseline은 업데이트의 기대값을 변화시키지는 않는다. 하지만 분산에는 큰 영향을 미친다. 어떤 state들에서는 모든 action들이 높은 값을 가지고, 다른 어떤 state들에서는 모든 action들이 낮은 값을 가질 수 있다. 이 때 baseline을 적절히 사용하면 모든 action들의 value와 baseline의 차이의 평균을 0으로 조정해 분산을 낮출 수 있다.

Actor-Critic Methods

REINFORCE는 앞서 봤듯이 MC method이기 때문에 여러 문제점을 가지고 있다. 우리는 이미 tabular method에서 봤듯이 MC method를 TD method로 개선할 수 있음을 알고 있다. 여기서도 마찬가지로 적용할 수 있다.

REINFORCE의 실제 return을 bootstrapping이 사용된 one-step return $G_{t:t+1}$으로 대체한다. one-step return은 획득한 reward와 next state에서의 discounted state value를 더한 값이다. baseline은 현재 state value로 설정한다. action을 평가하는데 state-value function이 이러한 방식으로 사용될 때 이를 critic이라고 부르며, policy 부분은 actor라고 부른다. 따라서 이러한 policy gradient method를 actor-critic method라고 부른다.

one-step actor-critic method는 one-step return과 baseline으로 학습된 state-value function을 통해 REINFORCE를 아래와 같이 완전히 대체할 수 있다.

\[\begin{align} \mathbf{\theta}_{t+1} &\doteq \mathbf{\theta}_t + \alpha \Big( G_{t:t+1} - \hat{v}(S_t, \mathbf{w}) \Big) \nabla \ln \pi(A_t \vert S_t, \mathbf{\theta}_t) \\ &= \mathbf{\theta}_t + \alpha \Big( R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w}) - \hat{v}(S_t, \mathbf{w}) \Big) \nabla \ln \pi(A_t \vert S_t, \mathbf{\theta}_t) \end{align}\]

state-value function을 학습하는 가장 자연스러운 방법은 semi-gradient TD(0)이다. actor-critic은 REINFORCE와 달리 bootstrapping을 이용하기 때문에 완전히 online으로 학습할 수 있다. 아래는 one-step actor-critic 알고리즘이다.

$\text{Algorithm: One-step Actor-Critic (episodic), for estimating $\pi_{\mathbf{\theta}} \approx \pi_\ast$}$

\(\begin{align*} & \textstyle \text{Input: a differentiable policy parameterization $\pi(a \vert s, \mathbf{\theta})$} \\ & \textstyle \text{Input: a differentiable state-value function parameterization $\hat{v}(s, \mathbf{w})$} \\ & \textstyle \text{Parameters: step sizes $\alpha^\mathbf{\theta} > 0$, $\alpha^\mathbf{w} > 0$} \\ & \textstyle \text{Initialize policy parameters $\mathbf{\theta} \in \mathbb{R}^{d'}$ and state-value weights $\mathbf{w} \in \mathbb{R}^d$ (e.g., to $\mathbf{0}$)} \\ \\ & \textstyle \text{Loop forever (for each episode)} \\ & \textstyle \qquad \text{Initialize $S$ (first state of episode)} \\ & \textstyle \qquad I \leftarrow 1 \\ & \textstyle \qquad \text{Loop while $S$ is not terminal (for each time step):} \\ & \textstyle \qquad\qquad A \sim \pi(\cdot \vert S, \mathbf{\theta}) \\ & \textstyle \qquad\qquad \text{Take action $A$, observe $S', R$} \\ & \textstyle \qquad\qquad \delta \leftarrow R + \gamma \hat{v}(S', \mathbf{w}) - \hat{v}(S, \mathbf{w}) \qquad \text{(if $S'$ is terminal, then $\hat{v}(S', \mathbf{w}) \doteq 0$)} \\ & \textstyle \qquad\qquad \mathbf{w} \leftarrow \mathbf{w} + \alpha^\mathbf{w} \delta \nabla \hat{v}(S, \mathbf{w}) \\ & \textstyle \qquad\qquad \mathbf{\theta} \leftarrow \mathbf{\theta} + \alpha^\mathbf{\theta} I \delta \nabla \ln \pi(A \vert S, \mathbf{\theta}) \\ & \textstyle \qquad\qquad I \leftarrow \gamma I \\ & \textstyle \qquad\qquad S \leftarrow S' \\ \end{align*}\)

Policy Parameterization for Continuous Actions

policy-based method는 큰 action space를 다루기에 적합하며 심지어 action이 무한개인 continuous action space를 다룰 수 있다. 수많은 action들의 각각의 확률을 학습하기 보다는, 확률 분포를 학습한다. 예를 들면 action이 실수 집합에서 정의될 때 action을 정규분포로부터 sampling 할 수 있다.

정규분포의 확률밀도함수는 일반적으로 아래와 같다.

\[p(x) \doteq \dfrac{1}{\sigma \sqrt{2\pi}} \exp \bigg(- \dfrac{(x - \mu)^2}{2 \sigma^2} \bigg)\]

$\mu$는 평균, $\sigma$는 표준편차이며, 여기서 $\pi$는 당연하지만 실수 $\pi \approx 3.14159$이다. $p(x)$는 확률이 아닌 $x$에서의 확률밀도이며, $x$가 어떤 범위 안에 있을 확률은 확률밀도함수의 integral이다. 아래 그림은 $\mu$와 $\sigma$의 값에 따른 정규분포 확률밀도함수이다.

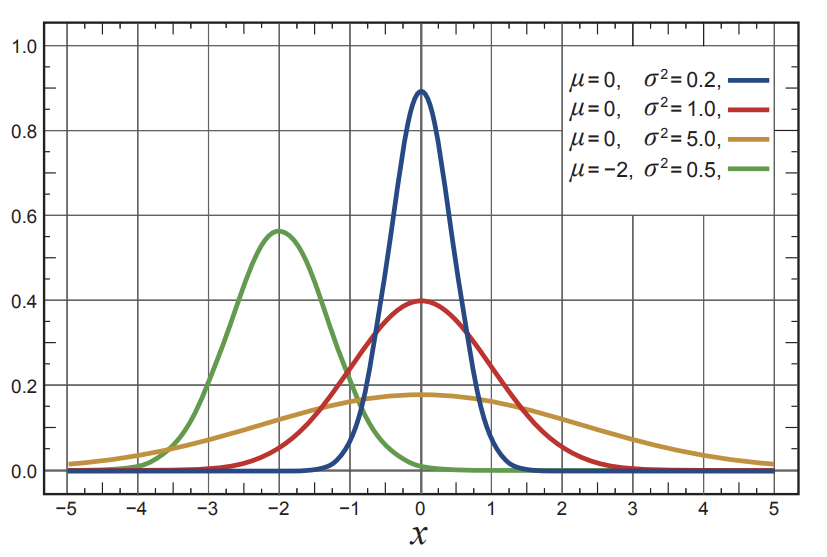Fig 2. Normal distribution.
(Image source: Sec 13.7 Sutton & Barto (2020).)

policy를 정규분포에 대해 매개변수화하기 위해 평균 $\mu$와 표준편차 $\sigma$를 아래와 같이 매개변수화한다.

\[\pi(a \vert s, \mathbf{\theta}) \doteq \dfrac{1}{\sigma(s, \mathbf{\theta}) \sqrt{2\pi}} \exp \bigg(- \dfrac{(a - \mu(s, \mathbf{\theta}))^2}{2 \sigma(s, \mathbf{\theta})^2} \bigg)\]

$\mu : \mathcal{S} \times \mathbb{R}^{d’} \rightarrow \mathbb{R}$와 $\sigma : \mathcal{S} \times \mathbb{R}^{d’} \rightarrow \mathbb{R}^+$는 매개변수화된 function approximator이다. 이를 위해 policy의 parameter vector를 $\mathbf{\theta} = [\mathbf{\theta} _\mu, \mathbf{\theta} _\sigma]^\top$와 같이 두 파트로 나누어야한다.

Summary

길고 긴 여정이 끝이 났다. 강화학습의 기초부터 policy gradient method까지 오는데 많은 시간이 걸렸다. 이 summary를 끝으로 RL Fundamental은 끝이다.

• policy gradient method는 policy 자체를 매개변수화하는 방법
• action을 선택하는 구체적인 확률을 학습할 수 있음
• discrete action 뿐만 아니라 continuous action에도 적용 가능
• policy gradient theorem에 의해 state distribution의 미분을 포함하지 않고 policy parameter에 의해 얼마나 성능이 영향을 받는지에 대한 기술이 가능
• policy gradient method에 baseline을 추가하면 분산을 낮추는데 상당히 도움이 됨
• REINFORCE는 Monte Carlo policy gradient method
• Actor-Critic은 bootstrapping을 통해 online 학습이 가능
• actor는 policy, critic은 state-value function을 학습

References

[1] Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction; 2nd Edition. 2020.

Footnotes

1. DevSlem. On-policy Prediction with Approximation. The Prediction Objective ($\overline{\text{VE}}$). On-policy Control with Approximation. Average Reward: A New Problem Setting for Continuing Tasks. Ergodicity. ↩

2. DevSlem. Finite Markov Decision Processes. What is MDPs. ↩

3. DevSlem. Finite Markov Decision Processes. Bellman Expectation Equation. ↩

4. Reinforcement Learning: An Introduction; 2nd Edition. 2020. Sec. 9.2, p.199. ↩