1. 개요
어떤 힘을 줘서 포물선 궤적으로 이동시키는 것 자체는 단순하다. 힘을 가하기만 하면 중력과의 상호작용에 의해 자연스럽게 포물선 운동을 한다. 하지만 내가 구현하고 싶은 것은 의도한 궤적으로 이동하는 포물선 운동이다. 단순히 힘을 주기만 하면 어느정도 높이로 올라가고 얼마나 멀리 가는지 알기 어렵다. 의도한 움직임을 구현할 수 있다면 더 정밀한 컨트롤이 가능해진다. 이를 한번 구현해보자.
2. 고려 사항
앞서 3차원이 아닌 2차원 상에서의 포물선 운동이라는 점을 미리 말하겠다. 2차원 포물선 운동은 고등학교를 나왔다면 충분히 이해할 수 있다.
먼저 고려해야할 사항을 알아보자.
- 어떤 방식으로 힘을 줄 것인가?
- 무엇을 기준으로 포물선 운동의 궤적을 정할 것인가?
위 사항에 대해 나는 아래와 같이 결정했다.
Rigidbody2D.AddForce()의mode매개변수에ForceMode2D.Impulse값을 준다. 이는 힘을 1번만 줘서 속도 변화의 즉각적 반영을 위한 것이다.- 포물선 운동을 가장 쉽게 특정할 수 있는 방법은 바로 최대 높이까지의 변위이다. 최대 높이의 위치가 결정된다면 그 포물선 운동은 유일하다. 그 이유는 2차함수를 생각하면 알 수 있다. 2차함수의 특징은 임의의 한 점과 꼭짓점이 있으면, 이 두 점을 지나는 유일한 2차함수를 결정할 수 있다.
3. 포물선 운동 알고리즘
포물선 운동의 특징
포물선 운동은 다음과 같은 특징을 가진다.
- 포물선 운동의 $x$성분은 등속도 운동을 한다.
- 포물선 운동의 $y$성분은 등가속도 운동을 한다.
- 최대 높이에서 $y$성분의 속도는 0이다.
위 특징은 굉장히 중요하다. 포물선 운동에서 각 성분은 독립적이기 때문에 $x$성분의 속도와 $y$성분의 속도를 따로 구할 것이다.
충격량
Rigidbody2D.AddForce()에 ForceMode2D.Impulse 모드로 힘을 가할 시 force 매개변수에는 충격량이 입력된다. 따라서 몇가지 물리 법칙을 활용하여 충격량을 구해야 한다.
충격량과 운동량의 변화량은 같다
충격량과 관련된 법칙이다. 충격량 $\vec{I} = \vec{F}t$이고 운동량 $\vec{p} = m\vec{v}$이며 이 때 아래와 같은 법칙을 얻을 수 있다.
\[\vec{I} = \Delta{\vec{p}}\] \[\vec{F}t = m\Delta{\vec{v}}\]즉, 충격량을 구하기 위해서는 운동량의 변화량을 구하면 되며, 질량은 이미 알고 있는 정보이기 때문에 결국 속도 변화만 알면 된다. 참고로 충격량과 운동량은 이름에 양이 들어가있다고 해서 스칼라가 아니다. 엄연한 벡터라는 점을 유의해야 한다.
알고리즘 구현하기
메서드 선언
위 2. 고려 사항에서 나는 최대 높이까지의 변위를 기준으로 포물선 운동을 구현하겠다고 했다. 즉, 우리는 매개변수로 최대 높이까지의 변위를 받을 것이다. 아래는 최대 높이까지의 변위이다.
\[\vec{s} = [d, h]\]아래는 위 정보를 바탕으로 선언한 메서드이다.
1
private void JumpForce(Vector2 maxHeightDisplacement) { }
최대 높이까지의 변위 정보를 Vector2 구조체 타입의 maxHeightDisplacement 매개변수에서 받는다.
역학적 에너지 보존 법칙
최대 높이까지의 변위는 이미 알고 있는 정보이다. 이 정보를 바탕으로 포물선 운동을 위한 각 성분의 처음 속도를 구할 수 있다. 중력계에서의 운동은 아래와 같은 법칙이 성립한다.
\[mgh = \displaystyle\frac{1}{2}mv^2\]맞다. 그 유명한 역학적 에너지 보존 법칙이다. 위 식을 보면 알겠지만 최대 높이 $h$만 알면 지면에서의 속도 $v$를 알 수 있다.
$y$성분의 처음 속도 $v_y$ 구하기
위 역학적 에너지 보존 법칙 식을 활용하자. 최대 높이까지의 변위는 이미 알고 있는 정보이기 때문에, 위 식을 $v$에 대해 정리하면 $y$성분의 속도 $v_y$를 구할 수 있다.
\[v_y = \pm\sqrt{2gh}\]우리가 구하려는 처음 속도 $v_y$는 $+\sqrt{2gh}$이다. $-\sqrt{2gh}$는 최대 높이에서 떨어졌을 때 지면에서의 속도이다.
아래는 위 수식을 적용한 코드이다.
1
2
3
4
Rigidbody2D rigid = this.rigid;
// m*k*g*h = m*v^2/2 (단, k == gravityScale) <= 역학적 에너지 보존 법칙 적용
float v_y = Mathf.Sqrt(2 * rigid.gravityScale * -Physics2D.gravity.y * maxHeightDisplacement.y);
위 식에서 중력가속도 $g$는 실제로 작용하는 중력가속도의 크기이기 때문에 Rigidbody2D.gravityScale 정보를 반영했다. 각 오브젝트마다 gravityScale이 다를 수 있기 때문이다. 따라서 중력가속도 $g$는 rigid.gravityScale * -Physics2D.gravity.y이다.
$x$성분의 속도 $v_x$ 구하기
$v_x$를 구하기 위해서는 속도에 대한 이해가 필요하다. 아래는 속도의 정의이다.
\[\vec{v}_{avg} = \displaystyle\frac{\vec{s}}{t}\]속도란 단위 시간당 이동거리이다. 중요한 것은 그냥 속도가 아닌 평균 속도이다. $x$성분은 등속도 운동이기 때문에 처음 속도가 곧 평균 속도이지만, $y$성분은 등가속도 운동이기 때문에 평균 속도를 구하는 과정이 필요하다.
그렇다면 왜 $y$성분의 평균 속도를 구하는가? 그 이유는 시간 $t$에 있다. 앞서 말했지만 우리는 이미 변위 정보를 알고 있다. 최대 높이까지 도달하는데 걸린 시간 $t$만 알 수 있다면 위 속도의 정의를 활용해 $v_x$를 구할 수 있다. 시간 $t$를 구하기 위해 우리는 동일한 시간 $t$동안 $x$성분은 등속도 운동으로, $y$성분은 등가속도 운동으로 최대 높이의 위치에 도달한다는 성질을 활용할 것이다. 아래 그림을 보자.
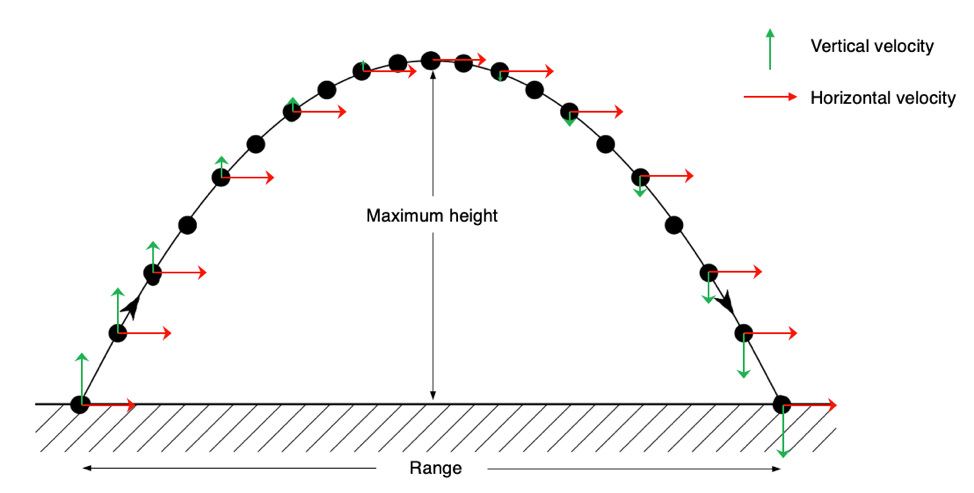
위 그림에서 각 포물선 위의 벡터의 $x$성분 크기는 유지되고, $y$성분은 최대 높이에서 크기가 0이 된다.
등가속도 운동의 특징 중 하나는 평균 속도가 처음 위치에서의 속도와 나중 위치에서의 속도의 평균이다. 이는 등가속도 운동에서 속도 그래프가 직선이기 때문이다. 이 사실을 활용해 $y$성분의 평균 속도를 구해보자.
처음 속도는 $v_y$이고 최대 높이에서의 속도는 $0$이다. 즉, 처음 위치에서 최대 높이까지 도달하는데 필요한 평균 속도는 $\displaystyle\frac{v_y}{2}$이다.
\[v_{avg} = \displaystyle\frac{v_y + 0}{2} = \displaystyle\frac{v_y}{2}\]평균 속도를 구했으니 이제 속도의 정의를 활용해 최대 높이까지 도달하는데 걸린 시간 $t$를 구할 수 있다.
\[t = \displaystyle\frac{s}{v_{avg}} = \displaystyle\frac{2h}{v_y}\]$y$성분에 대한 1차원 운동이기 때문에 내적을 쓸 필요 없이 나누기만 하면 된다.
이제 드디어 $x$성분의 속도를 구할 수 있다. $x$성분은 등속도 운동이기 때문에 처음속도가 곧 평균속도이다. 최대 높이까지의 $x$성분의 변위는 $d$이다.
\[s = d\] \[v_x = \displaystyle\frac{s}{t} = \displaystyle\frac{d}{2h}v_y\]아래는 위 식을 적용한 코드이다.
1
2
// 포물선 운동 법칙 적용
float v_x = maxHeightDisplacement.x * v_y / (2 * maxHeightDisplacement.y);
충격량을 구해 힘을 가하기
앞의 충격량과 운동량의 변화량은 같다에서 알아봤듯이 아래 법칙을 활용하여 충격량을 구할 것이다.
\[\vec{F}t = m\Delta{\vec{v}}\]$\Delta{\vec{v}}$는 변화시키고자 하는 속도를 위해 필요한 속도의 변화량으로 나중속도 - 처음속도이다. 처음 속도 $\vec{v_0}$는 원래 오브젝트가 가지고 있던 속도, 나중 속도는 우리가 직전에 구한 $\vec{v_1} = [v_x, v_y]$이다. 원래 속도를 가지고 있던 오브젝트에 힘을 줘 속도 $v$를 $\vec{v_1} = [v_x, v_y]$로 변화시켜야 우리가 원하는 포물선 운동이 구현된다. 속도의 변화량을 구하는 것은 간단하다.
위 정보를 종합하여 충격량을 구했다. 아래는 충격량을 구해 Rigidbody2D에 힘을 가하는 코드이다.
1
2
Vector2 force = rigid.mass * (new Vector2(v_x, v_y) - rigid.velocity);
rigid.AddForce(force, ForceMode2D.Impulse);
완성된 알고리즘
1
2
3
4
5
6
7
8
9
10
11
12
private void JumpForce(Vector2 maxHeightDisplacement)
{
Rigidbody2D rigid = this.rigid;
// m*k*g*h = m*v^2/2 (단, k == gravityScale) <= 역학적 에너지 보존 법칙 적용
float v_y = Mathf.Sqrt(2 * rigid.gravityScale * -Physics2D.gravity.y * maxHeightDisplacement.y);
// 포물선 운동 법칙 적용
float v_x = maxHeightDisplacement.x * v_y / (2 * maxHeightDisplacement.y);
Vector2 force = rigid.mass * (new Vector2(v_x, v_y) - rigid.velocity);
rigid.AddForce(force, ForceMode2D.Impulse);
}
4. 활용
코드
위 알고리즘을 활용해보겠다. 먼저 아래는 위 알고리즘을 활용한 간단한 코드이다.
위 코드에서 최대 높이인 maxHeightDisplacement를 필드로 선언했다. InterpolatedFunction은 대리자 타입으로 보간된 함수를 등록할 수 있다.
1
f = PhysicsUtility.NewtonPolynomial(Vector2.zero, maxHeightDisplacement, new Vector2(2 * maxHeightDisplacement.x, 0f)); // 2차함수 보간
Awake()에서 사용한 위 PhysicsUtility.NewtonPolynomial() 메서드는 매개변수로 입력한 점들을 지나는 유일한 다항함수를 반환하는 메서드이다. 이와 관련된 내용은 뉴턴 다항식 보간법에서 확인할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
private void DrawProjectileMotionLine()
{
float interval = 2 * maxHeightDisplacement.x / pointCount;
Vector2 current = Vector2.zero;
for (int i = 0; i < pointCount; i++)
{
float next_x = current.x + interval;
Vector2 next = new Vector2(next_x, f(next_x));
Debug.DrawLine(current + rigid.position, next + rigid.position, Color.green, 3f);
current = next;
}
}
위 메서드는 오브젝트가 움직이는 포물선 궤적을 Scene창에 그리기 위해 구현했다.
동작 장면
인스펙터
인스펙터 설정 화면이다.
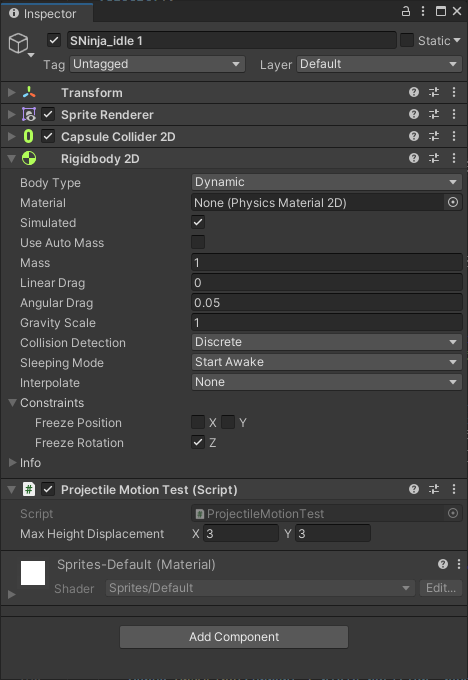
Max Height Displacement는 $(3, 3)$으로 지정했다. 아래는 각각 Gravity Scale 값에따른 동작 장면이다.
Gravity Scale: 1
정지 상태에서의 포물선 궤적으로의 점프이다.
.webp)
Gravity Scale: 2
.webp)
Gravity Scale: 4
.webp)
앞서 중력가속도 $g$를 구할 때 Rigidbody2D.gravityScale 정보를 반영했기 때문에 Gravity Scale 값에 관계 없이 의도한 포물선 궤적으로 이동하는 모습을 확인할 수 있다.
운동상태에서 다시 점프
Gravity Scale 값은 2.5이며 포물선 궤적으로 운동 중에 다시 한번 포물선 궤적의 점프를 시도했다. 원하는 궤적으로 정확히 운동하는 모습을 확인할 수 있다.
.webp)
위 충격량을 구해 힘을 가하기에서 속도 변화인 $\Delta{\vec{v}}$를 구한 이유가 바로 위와 같이 정지된 상태가 아닌 운동 상태에서 원하는 궤적으로 움직이기 위해서이다.